
 的
的 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案科目:初中数学 来源:不详 题型:单选题

A. | B. |
C. | D. |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,测得由点A看大树顶端
,测得由点A看大树顶端 的仰角为35°;在点
的仰角为35°;在点 和大树之间选择一点
和大树之间选择一点 (
( 、
、 、
、 在同一直线上),测得由点
在同一直线上),测得由点 看大树顶端
看大树顶端 的仰角恰好为45°;量出
的仰角恰好为45°;量出 、
、 两点间的距离为4.5米.
两点间的距离为4.5米. 的高度.(可能用到的参考数据:sin35°≈0.57 cos35°≈0.82 tan35°≈0.70).
的高度.(可能用到的参考数据:sin35°≈0.57 cos35°≈0.82 tan35°≈0.70).
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

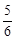 ,求AE的值.
,求AE的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com