

分析 (1)先利用旋转得出两个顶角相等的两个等腰三角形,即可得出结论;
(2)假设存在,然后利用确定的出AE=BE,即可求出∠A1AP=∠AA1P,最后用∠BAC=45°建立方程化简即可;
(3)先判断出△ABQ∽△CPB,得出比例式即可得出结论.
解答 解:(1)∵将△ABP绕点P按顺时针方向旋转α角(0°<α<180°),得到△A1B1P,
∴∠APA1=∠BPB1=α,AP=A1P,BP=B1P,
∴∠AA1P=∠A1AP=$\frac{180°-∠AP{A}_{1}}{2}$=$\frac{180°-α}{2}$,∠BB1P=∠B1BP=$\frac{180°-∠BP{B}_{1}}{2}$=$\frac{180°-α}{2}$,
∴∠PAA1=∠PBB1,
(2)假设在α角变化的过程中,存在△BEF与△AEP全等,
∵△BEF与△AEP全等,
∴AE=BE,
∴∠ABE=∠BAE=β,
∵AP=A1P,
∴∠A1AP=∠AA1P=$\frac{180°-α}{2}$,
∵AB=BC,∠ABC=90°,
∴∠BAC=45°,
∴β+$\frac{180°-α}{2}$=45°,
∴α-2β=90°,
(3)当α=90°时,
∵AP=A1P,BP=B1P,∠APA1=∠BPB2=90°,
∴∠A=∠PBB1=45°,
∵∠A=∠C,∠AQB=∠C+∠QBC=45°+∠QBC=∠PBC,
∴△ABQ∽△CPB,
∴$\frac{AQ}{BC}=\frac{AB}{PC}$,
∵AB=$\sqrt{2}$,
∴$\frac{2-y}{\sqrt{2}}=\frac{\sqrt{2}}{2-x}$,
∴y=$\frac{2x-2}{x-2}$.
点评 此题是几何变换综合题,主要考查了旋转的性质,等腰三角形的性质,全等三角形的性质,相似三角形的判定和性质,解(2)的关键是得出∠BAC=45°,解(3)的关键是判断出△ABQ∽△CPB,是一道很好的中考常考题.


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源:2016~2017学年安徽省芜湖市九年级下学期第一次模拟考试数学试卷(解析版) 题型:单选题
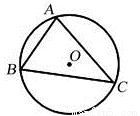
如图,⊙O是△ABC的外接圆,弦AC的长为3,sinB=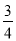 ,则⊙O的半径为( )
,则⊙O的半径为( )
A. 4 B. 3 C. 2 D. 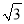
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,计划围一个面积为50m2的长方形场地,一边靠旧墙(墙长为10m),另外三边用篱笆围成,并且它的长与宽之比为5:2.讨论方案时,小英说:“我们不可能围成满足要求的长方形场地.”小军说:“面积和长宽比例是确定的,肯定可以围得出来.”请你判断谁的说法正确,为什么?
如图,计划围一个面积为50m2的长方形场地,一边靠旧墙(墙长为10m),另外三边用篱笆围成,并且它的长与宽之比为5:2.讨论方案时,小英说:“我们不可能围成满足要求的长方形场地.”小军说:“面积和长宽比例是确定的,肯定可以围得出来.”请你判断谁的说法正确,为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC,动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发,沿射线AC方向以每秒3个单位的速度运动,过点D作DH⊥AB于H,过点E作EF上AC交射线BB1于F,G是EF中点,连接DG,设点D运动的时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC,动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发,沿射线AC方向以每秒3个单位的速度运动,过点D作DH⊥AB于H,过点E作EF上AC交射线BB1于F,G是EF中点,连接DG,设点D运动的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
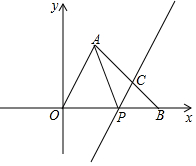 如图,将△OAB放在平面直角坐标系中,O为原点,点A(2,4),点B(6,0)在边OB上有一动点P,过P作PC∥OA交AB于C,连接AP.
如图,将△OAB放在平面直角坐标系中,O为原点,点A(2,4),点B(6,0)在边OB上有一动点P,过P作PC∥OA交AB于C,连接AP.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高22米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有25米的距离(B,F,C在一条直线上).
如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高22米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有25米的距离(B,F,C在一条直线上).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AE∥BF,AC平分∠BAE,交BF于C.
如图,AE∥BF,AC平分∠BAE,交BF于C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com