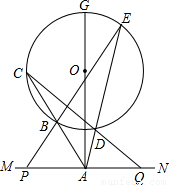
证明:作E点关于GA的对称点F,连FQ、FA,FC,
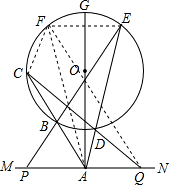
∵OA⊥MN,EF⊥OA,
则有∠FAP=∠EAQ,∠EAP=∠FAQ,FA=EA,
∵E,F,C,D共圆
∴∠PAF=∠AFE=∠AEF=180°-∠FCD,
∵∠PAF=180-∠FAQ,
∴∠FCD=∠FAQ,
∴FCAQ四点共圆,
∠AFQ=∠ACQ=∠BED,
在△EPA和△FQA中
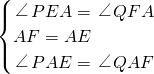
,
∴△EPA≌△FQA,
∴AP=AQ.
分析:作E点关于GA的对称点F,连FQ、FA,FC,根据轴对称和平行线性质推出∠FAP=∠EAQ,∠EAP=∠FAQ,FA=EA,求出∠FCQ=∠FAQ,推出FCAQ四点共圆,推出∠PEA=∠QFA,根据ASA推出△PEA和△QFA全等即可.
点评:本题综合考查了全等三角形的判定和性质,平行线的性质,轴对称的性质,圆内接四边形的性质,圆周角定理,垂线等知识点,解此题的关键是求出∠AEP=∠AFQ,题型较好,有一定的难度,通过做题培养了学生分析问题的能力,符合学生的思维规律,证两线段相等,一般考虑证所在的两三角形全等.

 设MN是圆O外一直线,过O作OA⊥MN于A,自A引圆的两条直线,交圆于B、C及D、E,直线EB及CD分别交MN于P、Q.
设MN是圆O外一直线,过O作OA⊥MN于A,自A引圆的两条直线,交圆于B、C及D、E,直线EB及CD分别交MN于P、Q.
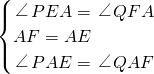 ,
,