
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,AE是经过A点的一条直线,且B,C在AE的两侧,BD⊥AE于D,CE⊥AE于E,CE=2,BD=6,则DE的长为.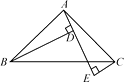
科目:初中数学 来源: 题型:
【题目】如图,抛物线C1:y=x2+bx+c经过原点,与x轴的另一个交点为(2,0),将抛物线C1向右平移m(m>0)个单位得到抛物线C2 , C2交x轴于A,B两点(点A在点B的左边),交y轴于点C.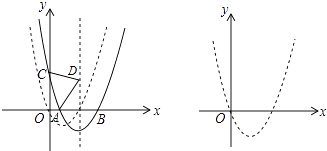
(1)求抛物线C1的解析式及顶点坐标;
(2)以AC为斜边向上作等腰直角三角形ACD,当点D落在抛物线C2的对称轴上时,求抛物线C2的解析式;
(3)若抛物线C2的对称轴存在点P,使△ PAC为等边三角形,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于M,则点M的表示的数为________________.
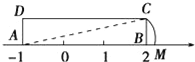
【答案】![]()
【解析】AC=AM=![]() =
=![]() ,∴AM=
,∴AM=![]()
【题型】填空题
【结束】
11
【题目】在△ABC中,AB=10,AC=2![]() ,BC边上的高AD=6,则另一边BC等于_______.
,BC边上的高AD=6,则另一边BC等于_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,AD是BC边上的中线,点E在AC上,且∠CDE=20°,现将△CDE沿直线DE折叠得到△FDE,连结BF.∠BFE的度数是.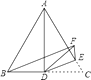
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:我们学过一次函数的图象的平移,如:将一次函数![]() 的图象沿x轴向右平移1个单位长度可得到函数
的图象沿x轴向右平移1个单位长度可得到函数![]() 的图象,再沿y轴向上平移1个单位长度,得到函数
的图象,再沿y轴向上平移1个单位长度,得到函数![]() 的图象;如果将一次函数
的图象;如果将一次函数![]() 的图象沿x轴向左平移1个单位长度可得到函数
的图象沿x轴向左平移1个单位长度可得到函数![]() 的图象,再沿y轴向下平移1个单位长度,得到函数
的图象,再沿y轴向下平移1个单位长度,得到函数![]() 的图象;仿照上述平移的规律,解决下列问题:
的图象;仿照上述平移的规律,解决下列问题:
![]() 将一次函数
将一次函数![]() 的图象沿x轴向右平移3个单位长度,再沿y轴向上平移1个单位长度,得到函数的图象;
的图象沿x轴向右平移3个单位长度,再沿y轴向上平移1个单位长度,得到函数的图象;
![]() 将
将![]() 的函数图象沿y轴向下平移3个单位长度,得到函数的图象,再沿x轴向左平移1个单位长度,得到函数的图象;
的函数图象沿y轴向下平移3个单位长度,得到函数的图象,再沿x轴向左平移1个单位长度,得到函数的图象;
![]() 函数
函数![]() 的图象可由
的图象可由![]() 的图象经过怎样的平移变换得到?
的图象经过怎样的平移变换得到?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AC,AD=AE,若添加一个条件不能得到“△ABD≌△ACE”是( )
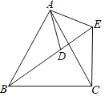
A. ∠ABD=∠ACE B. BD=CE C. ∠BAD=∠CAE D. ∠BAC=∠DAE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于实数a,b,定义运算“*”:a*b=a2-ab(a≤b); a*b=b2-ab(a>b),关于x的方程(2x-1)*(x-1)=m 恰好有三个不相等的实数根,则m的取值范围是( )
A.m> ![]()
B. ![]()
C. ![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按 ![]() 元销售时,每天可销售
元销售时,每天可销售 ![]() 个;若销售单价每降低元,每天可多售出
个;若销售单价每降低元,每天可多售出 ![]() 个.已知每个玩具的固定成本为
个.已知每个玩具的固定成本为 ![]() 元,问这种玩具的销售单价为多少元时,厂家每天可获利润
元,问这种玩具的销售单价为多少元时,厂家每天可获利润 ![]() 元?
元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com