
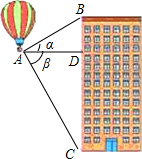
 如图,热气球探测器显示,从热气球A处看一栋楼顶部B处的仰角为30°,看这栋楼底部C处的俯角为60°,热气球与楼的水平距离AD为100米,试求这栋楼的高度BC.
如图,热气球探测器显示,从热气球A处看一栋楼顶部B处的仰角为30°,看这栋楼底部C处的俯角为60°,热气球与楼的水平距离AD为100米,试求这栋楼的高度BC. 分析 在直角三角形ADB中和直角三角形ACD中,根据锐角三角函数中的正切可以分别求得BD和CD的长,从而可以求得BC的长,本题得以解决.
解答 解:由题意可得,
α=30°,β=60°,AD=100米,∠ADC=∠ADB=90°,
∴在Rt△ADB中,α=30°,AD=100米,
∴tanα=$\frac{BD}{AD}$=$\frac{BD}{100}$=$\frac{\sqrt{3}}{3}$,
∴BD=$\frac{100\sqrt{3}}{3}$米,
在Rt△ADC中,β=60°,AD=100米,
∴tanβ=$\frac{CD}{AD}=\frac{CD}{100}=\sqrt{3}$,
∴CD=100$\sqrt{3}$米,
∴BC=BD+CD=$\frac{100\sqrt{3}}{3}+100\sqrt{3}=\frac{400\sqrt{3}}{3}$米,
即这栋楼的高度BC是$\frac{400\sqrt{3}}{3}$米.
点评 本题考查解直角三角形的应用-仰角俯角问题、锐角三角函数,解答此类问题的关键是明确题意,利用锐角三角函数解答.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:解答题
 某企业生产并销售某种产品,假设销售量与产量相等,图中的折线ABD、线段CD分别表示该产品每千克生产成本y1(元)、销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.
某企业生产并销售某种产品,假设销售量与产量相等,图中的折线ABD、线段CD分别表示该产品每千克生产成本y1(元)、销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,已知△ABC中,∠BAC=90°,AB=AC,MN是经过点A的直线,BD⊥MN,CE⊥MN,垂足分别为点D、E.
如图所示,已知△ABC中,∠BAC=90°,AB=AC,MN是经过点A的直线,BD⊥MN,CE⊥MN,垂足分别为点D、E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
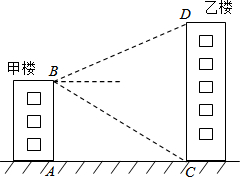 如图,甲、乙两楼的距离AC=30m,甲楼高AB=40m,自甲楼楼顶的B处看乙楼楼顶的D处,仰角为28°,求乙楼的高CD的长.(结果精确到0.1m,参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)
如图,甲、乙两楼的距离AC=30m,甲楼高AB=40m,自甲楼楼顶的B处看乙楼楼顶的D处,仰角为28°,求乙楼的高CD的长.(结果精确到0.1m,参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com