
 如图,在梯形ABCD中,AB∥CD,AD=DC=CB,AC⊥BC,那么下列结论不正确的是( )
如图,在梯形ABCD中,AB∥CD,AD=DC=CB,AC⊥BC,那么下列结论不正确的是( )| A. | AC=2CD | B. | DB⊥AD | C. | ∠ABC=60° | D. | ∠DAC=∠CAB |
分析 A、根据三角形的三边关系即可得出A不正确;B、通过等腰梯形的性质结合全等三角形的判定与性质即可得出∠ADB=90°,从而得出B正确;C、由梯形的性质得出AB∥CD,结合角的计算即可得出∠ABC=60°,即C正确;D、由平行线的性质结合等腰三角形的性质即可得出∠DAC=∠CAB,即D正确.综上即可得出结论.
解答 解:A、∵AD=DC,
∴AC<AD+DC=2CD,A不正确;
B、∵在梯形ABCD中,AD=CB,
∴梯形ABCD为等腰梯形,
∴∠DAB=∠CBA.
在△DAB和△CBA中,$\left\{\begin{array}{l}{AD=BC}\\{∠DAB=∠CBA}\\{AB=BA}\end{array}\right.$,
∴△DAB≌△CBA(SAS),
∴∠ADB=∠BCA.
∵AC⊥BC,
∴∠ADB=∠BCA=90°,
∴DB⊥AD,B成立;
C、∵AB∥CD,
∴∠CDB=∠ABD,∠ABC+∠DCB=180°,
∵DC=CB,
∴∠CDB=∠CBD=∠ABD,
∵∠ACB=90°,
∴∠CDB=∠CBD=∠ABD=30°,
∴∠ABC=∠ABD+∠CBD=60°,C正确;
D、∵AB∥CD,
∴∠DCA=∠CAB,
∵AD=DC,
∴∠DAC=∠DCA=∠CAB,D正确.
故选A.
点评 本题考查了梯形的性质、平行线的性质、等腰三角形的性质以及全等三角形的判定与性质,解题的关键是逐项分析四个选项的正误.本题属于中档题,稍显繁琐,但好在该题为选择题,只需由三角形的三边关系得出A不正确即可.


科目:初中数学 来源: 题型:解答题
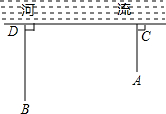 如图,草原上,一牧童在A处放马,牧童家在B处,A、B处距河岸的距离AC,BD的长分别为500m和700m,且CD=500m,天黑前牧童从A点将马牵到河边去饮水后,再赶回家,牧童将马牵到河边什么地方饮水,才能使走过的路程最短?牧童最少要走多少m?
如图,草原上,一牧童在A处放马,牧童家在B处,A、B处距河岸的距离AC,BD的长分别为500m和700m,且CD=500m,天黑前牧童从A点将马牵到河边去饮水后,再赶回家,牧童将马牵到河边什么地方饮水,才能使走过的路程最短?牧童最少要走多少m?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 解不等式组:$\left\{\begin{array}{l}{5x+2>3(x-1)①}\\{\frac{1}{2}x-1≤7-\frac{3}{2}x②}\end{array}\right.$,请结合题意填空,完成本题的解答.
解不等式组:$\left\{\begin{array}{l}{5x+2>3(x-1)①}\\{\frac{1}{2}x-1≤7-\frac{3}{2}x②}\end{array}\right.$,请结合题意填空,完成本题的解答.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com