
 如图,一条笔直的公路l穿过草原,公路边有一消防站A,距离公路5千米的地方有一居民点B,A、B的直线距离是13千米.一天,居民点B着火,消防员受命欲前往救火,若消防车在公路上的最快速度是80千米/小时,而在草地上的最快速度是40千米/小时,则消防车在出发后最快经过$\frac{5\sqrt{3}+12}{80}$小时可到达居民点B.(友情提醒:消防车可从公路的任意位置进入草地行驶.)
如图,一条笔直的公路l穿过草原,公路边有一消防站A,距离公路5千米的地方有一居民点B,A、B的直线距离是13千米.一天,居民点B着火,消防员受命欲前往救火,若消防车在公路上的最快速度是80千米/小时,而在草地上的最快速度是40千米/小时,则消防车在出发后最快经过$\frac{5\sqrt{3}+12}{80}$小时可到达居民点B.(友情提醒:消防车可从公路的任意位置进入草地行驶.) 分析 要求所用行车时间最短,就要计算好行驶的路线,可以设在公路上行驶x千米,根据题意,找出可以运用勾股定理的直角三角形,运用勾股定理求解.
解答  解:如图所示,公路上行驶的路线是AD,草地上行驶的路线是DB,设AD的路程为x千米,
解:如图所示,公路上行驶的路线是AD,草地上行驶的路线是DB,设AD的路程为x千米,
由已知条件AB=13千米,BC=5千米,BC⊥AC,知
AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=12千米.
则CD=AC-AD=(12-x)千米,
BD=$\sqrt{C{D}^{2}+B{C}^{2}}$=$\sqrt{(12-x)^{2}+{5}^{2}}$km,
设走的行驶时间为y,则
y=$\frac{x}{80}$+$\frac{\sqrt{(12-x)^{2}+25}}{40}$.
整理为关于x的一元二次方程得
3x2+(160y-96)x-6400y2+676=0.
因为x必定存在,所以△≥0.即
(160y-96)2-4×3×(676-6400y2)≥0.
化简得3400y2-6400y+23≥0.
解得y≥$\frac{5\sqrt{3}+12}{80}$.
故答案为:$\frac{5\sqrt{3}+12}{80}$.
点评 本题考查的是在直角三角形中勾股定理的运用,画出图形构建直角三角形是关键,根据一元二次不等式的求解,可以计算出解的最小值,以便求出最短路程.


科目:初中数学 来源: 题型:填空题
 如图,从边长为30cm的等边△ABC纸片中剪出面积为100$\sqrt{3}$cm2的长方形纸片DEFG,为了更充分的利用剪剩下的纸片△ADG,则能剪出的最大的长方形纸片HIJK的面积为50$\sqrt{3}$cm2.
如图,从边长为30cm的等边△ABC纸片中剪出面积为100$\sqrt{3}$cm2的长方形纸片DEFG,为了更充分的利用剪剩下的纸片△ADG,则能剪出的最大的长方形纸片HIJK的面积为50$\sqrt{3}$cm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,二次函数y=ax2+2x+c的图象与x轴交于点A(-1,0)和点B,与y轴交于点C(0,3).
如图,二次函数y=ax2+2x+c的图象与x轴交于点A(-1,0)和点B,与y轴交于点C(0,3).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
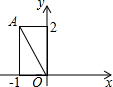 如图,已知点A(-1,2),将线段OA绕O点顺时针方向旋转90°后,得到线段OA′,则点A′的坐标是( )
如图,已知点A(-1,2),将线段OA绕O点顺时针方向旋转90°后,得到线段OA′,则点A′的坐标是( )| A. | (-3,-2) | B. | (2,2) | C. | (3,0) | D. | (2,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,含有30°的Rt△AOB的斜边OA在y轴上,且BA=3,∠AOB=30°,将Rt△AOB绕原点O顺时针旋转一定的角度,使直角顶点B落在x轴的正半轴上,得相应的△A′OB′,则A点运动的路程长是( )
如图,含有30°的Rt△AOB的斜边OA在y轴上,且BA=3,∠AOB=30°,将Rt△AOB绕原点O顺时针旋转一定的角度,使直角顶点B落在x轴的正半轴上,得相应的△A′OB′,则A点运动的路程长是( )| A. | 4π | B. | 5π | C. | 6π | D. | 7π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
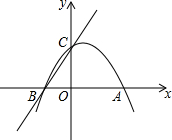 如图所示,二次函数y1=-x2+nx+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C(0,3).
如图所示,二次函数y1=-x2+nx+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C(0,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:关于x的一元二次方程ax2-2(a-1)x+a-2=0(a>0).
已知:关于x的一元二次方程ax2-2(a-1)x+a-2=0(a>0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
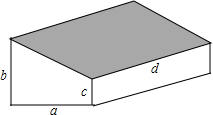 如图,要修建一个蔬菜大棚,棚的横截面是直角梯形,棚宽a=6米,棚高分别为b=5米,c=2米,长为d=30米,现要在棚顶覆盖塑料膜(即图中阴影部分),求共计需要塑料膜多少平方米?
如图,要修建一个蔬菜大棚,棚的横截面是直角梯形,棚宽a=6米,棚高分别为b=5米,c=2米,长为d=30米,现要在棚顶覆盖塑料膜(即图中阴影部分),求共计需要塑料膜多少平方米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
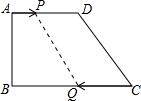 如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=18cm,BC=21cm,点P从点A开始沿AD边向D以1cm/s的速度运动,点Q从C点开始沿CB边向B以2cm/s的速度运动,如果P、Q分别从A、C同时出发,设运动时间为t秒.
如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=18cm,BC=21cm,点P从点A开始沿AD边向D以1cm/s的速度运动,点Q从C点开始沿CB边向B以2cm/s的速度运动,如果P、Q分别从A、C同时出发,设运动时间为t秒.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com