
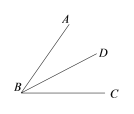
【题目】如图,已知BD平分∠ABC. 请补全图形后,依条件完成解答.
(1)在直线BC下方画∠CBE,使∠CBE与∠ABC互补;
(2)在射线BE上任取一点F,过点F画直线FG∥BD交BC于点G;
(3)判断∠BFG与∠BGF的数量关系,并说明理由.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,AD∥BC,AF平分∠BAD交BC于点F,BE平分∠ABC交AD于点E.求证: 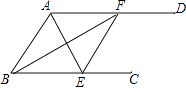
(1)△ABF是等腰三角形;
(2)四边形ABFE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+bx+3(a≠0)与x轴、y轴分别交于点A(﹣1,0)、B(3,0)、点C三点.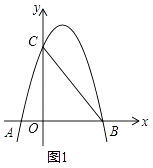
(1)试求抛物线的解析式;
(2)点D(2,m)在第一象限的抛物线上,连接BC,BD.试问,在对称轴左侧的抛物线上是否存在一点P,满足∠PBC=∠DBC?如果存在,请求出点P点的坐标;如果不存在,请说明理由;
(3)如图2,在(2)的条件下,将△BOC沿x轴正方向以每秒1个单位长度的速度向右平移,记平移后的三角形为△B′O′C′.在平移过程中,△B′O′C′与△BCD重叠的面积记为S,设平移的时间为t秒,试求S与t之间的函数关系式?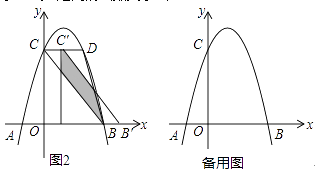
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】ABCD中,E是CD边上一点,
(1)将△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,如图1所示.观察可知:与DE相等的线段是 ,∠AFB=∠
(2)如图2,正方形ABCD中,P、Q分别是BC、CD边上的点,且∠PAQ=45°,试通过旋转的方式说明:DQ+BP=PQ;
(3)在(2)题中,连接BD分别交AP、AQ于M、N,你还能用旋转的思想说明BM2+DN2=MN2吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长交AD于E,交BA的延长线于点F.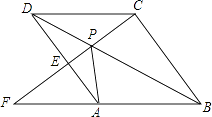
(1)求证:△APD≌△CPD;
(2)求证:△APE∽△FPA;
(3)猜想:线段PC,PE,PF之间存在什么关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】麒麟区第七中学现有一块空地ABCD如图所示,现计划在空地上种草皮,经测量,∠B=90°,AB=3m,BC=4m,CD=13m,AD=12m.

(1)求出空地ABCD的面积?
(2)若每种植1平方米草皮需要300元,问总共需投入多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a,b,c在数轴上的位置如图所示,且表示数a的点、数b的点与原点的距离相等.
(1)用“>”“<”或“=”填空:b______0,a+b______0,a-c______0,b-c______0;
(2)|b-1|+|a-1|=________;
(3)化简:|a+b|+|a-c|-|b|+|b-c|.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,取点D与点E,使得AD=AE,∠BAE=∠CAD,连结BD与CE交于点O.求证:

(1)△ABD≌△ACE;
(2)OB=OC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com