
【题目】如图,在等边三角形ABC中,BC=6 cm,射线AG∥BC,点E从点A出发沿射线AG以1 cm/s的速度运动;同时点F从点B出发沿射线BC以2 cm/s的速度运动.设运动时间为t(s).
(1)△ABC的BC边上的高为_________cm;
(2)连接EF,当EF经过AC的中点D时,求证:△ADE≌△CDF;
(3)求当t为何值时,AC与EF互相平分;
(4)当t=________s时,四边形ACFE是菱形.

【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() ;(4)6
;(4)6
【解析】
(1)根据等边三角形三线合一即可求解;
(2)由题意得到AD=CD,再由AG与BC平行,利用两直线平行内错角相等得到两对角相等,利用AAS即可得证;
(3)根据AC与EF互相平分,可得△ADE≌△CDF,可得AE=CF即![]() ,故可求解;
,故可求解;
(4)若四边形ACFE是菱形,则有CF=AC=AE=6,由E的速度求出E运动的时间即可.
解:(1)如图,过A点作AH⊥BC于H点
∵△ABC是等边三角形,BC=6 cm
∴BH=![]() BC=3cm
BC=3cm
∴AH=![]() =
=![]() cm
cm
故答案为:![]() .
.

(2)证明:∵AG∥BC,
∴∠EAD=∠DCF,∠AED=∠DFC,
∵D为AC的中点,
∴AD=CD,
在△ADE和△CDF中,
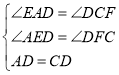 ,
,
∴△ADE≌△CDF(AAS);
(3)若AC与EF互相平分,
则AD=CD,ED=FD,又∠ADE=∠CDF
∴△ADE≌△CDF.
∴AE=CF.
∴![]() .
.
解得![]() .
.
(4)若四边形ACFE是菱形,则有CF=AC=AE=6,
则此时的时间t=6÷1=6(s).
故答案为:6.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
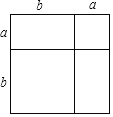
【题目】如图所示的大正方形是由两个小正方形和两个长方形组成.
(1)通过两种不同的方法计算大正方形的面积,可以得到一个数学等式;
(2)利用(1)中得到的结论,解决下面的问题:若a+b=2,ab=﹣3,
求:①a2+b2;
②a4+b4.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】几何探究题
(1)发现:在平面内,若BC=a,AC=b,其中a>b.
当点A在线段BC上时(如图1),线段AB的长取得最小值,最小值为 ;
当点A在线段BC延长线上时(如图2),线段AB的长取得最大值,最大值为 .
(2)应用:点A为线段BC外一动点,如图3,分别以AB、AC为边,作等边△ABD和等边△ACE,连接CD、BE.
①证明:CD=BE;
②若BC=3,AC=1,则线段CD长度的最大值为 .
(3)拓展:如图4,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线AB外一动点,且PA=2,PM=PB,∠BPM=90°.请直接写出线段AM长的最大值及此时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用若干块如左图所示的正方形或长方形纸片拼成图(1)和图(2)
(1)如图(1),若AD=7,AB=8,求![]() 与
与![]() 的值;
的值;
(2)如图(1),若长方形ABCD的面积为35,其中阴影部分的面积为20,求长方形ABCD的周长;

图(1)
(3)如图(2),若AD的长度为5,AB的长度为![]() .
.

图(2)
①当![]() =________,
=________,![]() =_________时,
=_________时,![]() ,
,![]() 的值有无数组;
的值有无数组;
②当![]() ________,
________,![]() _________时,
_________时,![]() ,
,![]() 的值不存在.
的值不存在.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2014年“元旦”前夕,某商场试销一种成本为30元的文化衫,经试销发现,若每件按34元的价格销售,每天能卖出36件;若每件按39元的价格销售,每天能卖出21件.假定每天销售件数y(件)是销售价格x(元)的一次函数.
(1)直接写出y与x之间的函数关系式y= .
(2)在不积压且不考虑其他因素的情况下,每件的销售价格定为多少元时,才能使每天获得的利润P最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
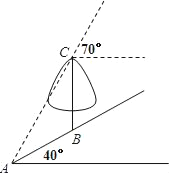
【题目】如图,在一个坡角为40°的斜坡上有一棵树BC,树高4米.当太阳光AC与水平线成70°角时,该树在斜坡上的树影恰好为线段AB,求树影AB的长.(结果保留一位小数)
(参考数据:sin20°=0.34,tan20°=0.36,sin30°=0.50,tan30°=0.58,sin40°=0.64,tan40°=0.84,sin70°=0.94,tan70°=2.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC=∠ACB,AD、BD分别平分△ABC的外角∠EAC、内角∠ABC,以下结论:① AD∥BC;②∠ACB=2∠ADB;③ BD⊥AC;④ AC=AD.其中正确的结论有( )
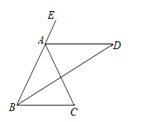
A.①②B.①②④C.①②③D.①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com