
分析 (1)先化简式子,再合并同类项即可解答本题;
(2)根据积的乘方和合并同类项可以解答本题;
(3)根据单项式乘多项式可以解答本题;
(4)根据多项式除以单项式可以解答本题.
解答 解(1)$\sqrt{25}$-$\root{3}{-8}$+|-$\sqrt{2}$|
=5-(-2)+$\sqrt{2}$
=7+$\sqrt{2}$;
(2)2a•3a2+(-2a)3
=6a3+(-8a3)
=-2a3;
(3)(-2x)•(3x2-$\frac{1}{2}$x+2)
=-6x3+x2-4x;
(4)(8a3-12a2b2)÷(2a)2
=(8a3-12a2b2)÷(4a2)
=2a-3b2.
点评 本题考查整式的混合运算、实数的运算,解题的关键是明确题意,找出所求问题需要的条件.


科目:初中数学 来源: 题型:解答题
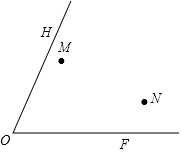 现有M和N两个村庄,欲在其旁两条公路OH、OF上建立A、B两个候车厅,使MA+AB+BN距离最小,请你在OH、OF上确定A、B两点的位置(保留作图痕迹)
现有M和N两个村庄,欲在其旁两条公路OH、OF上建立A、B两个候车厅,使MA+AB+BN距离最小,请你在OH、OF上确定A、B两点的位置(保留作图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,平面直角坐标系中,每个小正方形边长都是1.
如图,平面直角坐标系中,每个小正方形边长都是1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com