
【题目】如图,在![]() 中,
中,![]() 于
于![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,
,![]() .
.

(1)如图1,求证:![]() ;
;
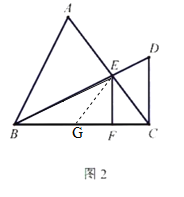
(2)如图2,![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(3)如图3,点![]() 在
在![]() 的延长线上,
的延长线上,![]() 于点
于点![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,当
,当![]() 的面积为
的面积为![]() 时, 求
时, 求![]() 的长.
的长.
【答案】(1)见解析;(2)图见解析;(3)![]() .
.
【解析】
(1)根据三角形内角和定理和对顶角的性质得到∠ABE=∠DCE,根据等边对等角得到∠BAC=∠ABC,利用角的和差即可得出结论;
(2)在FB上截取FG=FC,连接EG.证明△EFG≌△EFC,得到EG=EC,∠EGC=∠ECG.再由三角形外角的性质得到∠EBG=∠BEG,由等角对等边得到BG=GE,进而有EC=BG,根据等式的性质即可得到AE=CG=2FC.
(3)作GN∥AC交AB的延长线于N,延长RA、CD交于点P.证明△GHC≌△CAP(ASA),根据全等三角形的性质得到GC=CP,CH=AP.通过证明△KGN∽△BCD,得到![]() ,从而得到KG=KH,则可以证明△KGN≌△KHA,由全等三角形的性质得到AH=GN=GB,根据线段的和差得到CH=PD,从而得到AP=CH=PD.设AP=x,AH=y,则CH=PD=x,GN=GB=y,CD=2y.在Rt△APC中,根据勾股定理求得x=3y,得到AC=x+y=4y,由平行线分线段成比例定理得到
,从而得到KG=KH,则可以证明△KGN≌△KHA,由全等三角形的性质得到AH=GN=GB,根据线段的和差得到CH=PD,从而得到AP=CH=PD.设AP=x,AH=y,则CH=PD=x,GN=GB=y,CD=2y.在Rt△APC中,根据勾股定理求得x=3y,得到AC=x+y=4y,由平行线分线段成比例定理得到![]() ,故
,故![]() ,由
,由![]() ,从而求得y的值.由BC=AC=4y即可得出结论.
,从而求得y的值.由BC=AC=4y即可得出结论.
(1)∵∠BAC=∠BDC,∠AEB=∠DEC,
∴∠ABE=∠DCE.
∵AC=BC,
∴∠BAC=∠ABC,
∴2∠ABC+∠BCA=180°,
∴2(∠ABE+∠DBC)+∠BCA=180°.
∵CD⊥CB,
∴∠BCD=90° ,
∴∠BCA+∠DCE=90°,
∴2∠BCA+2∠DCE=180°,
∴2∠BCA+2∠ABE=180°,
∴2∠BCA+2∠ABE=2(∠ABE+∠DBC)+∠BCA,
∴∠BCA=2∠DBC,
∴∠ECB=2∠EBC;
(2)在FB上截取FG=FC,连接EG.
∵EF⊥BC,
∴∠EFG=∠EFC=90°.
在△EFG和△EFC中,∵EF=EF,∠EFG=∠EFC,GF=FC,
∴△EFG≌△EFC,
∴EG=EC,∠EGC=∠ECG.
∵∠ECB=2∠EBC,
∴∠EGC=2∠EBC.
∵∠EBG+∠BEG=∠EGC,
∴∠EBG+∠BEG=2∠EBG,
∴∠EBG=∠BEG,
∴BG=GE,
∴EC=BG.
∵AC=BC,
∴AE=CG=2FC.
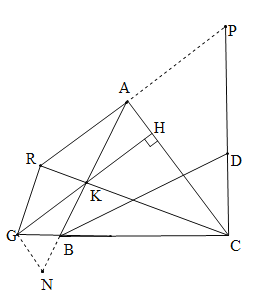
(3)如图,作GN∥AC交AB的延长线于N,延长RA、CD交于点P.
∵GH⊥AC,
∴∠AHG=∠CHG=90°,
∴∠HCG+∠CGH=90°.
∵AR∥GH,
∴∠PAC=∠AHG=90°,
∴∠PAC=∠CHG.
∵CD⊥BC,
∴∠PCA+∠HCG=90°,
∴∠PCA=∠CGH.
在△GHC和△CAP中,
∵∠GHC=∠CAP,GH=CA,∠CGH=∠PCA,
∴△GHC≌△CAP(ASA).
∴GC=CP,CH=AP.
∵AC=BC,
∴∠CBA=∠CAB=∠CDB.
∵GN∥AC,
∴∠N=∠CAB,
∴∠N=∠CAB=∠CBA=∠GBN=∠CDB,
∴GN=GB.
∵GH⊥AC,GN∥AC,
∴∠KGN=90°=∠DCB,
∴△KGN∽△BCD,
∴![]() ,
,
∴KG=![]() BC=
BC=![]() AC=
AC=![]() GH,
GH,
∴KG=KH.
∵∠AHK=∠KGN=90°,∠HAK=∠N,KG=KH,
∴△KGN≌△KHA,
∴AH=GN=GB,
∴CH=AC-AH=BC-GB=CG-2GB=CG-CD=PD,
∴AP=CH=PD.
设AP=x,AH=y,则CH=PD=x,GN=GB=y,CD=2y.
在Rt△APC中,![]() ,
,
解得:x=3y或x= -y(舍去),
∴AC=x+y=4y.
∵AR∥HK,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴y=![]() 或y=
或y=![]() (舍去),
(舍去),
∴BC=AC=4y=6.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=6,点D是BC边上一动点(不与B、C重合),过点D作DE⊥BC交AB边于点E,将∠B沿直线DE翻折,点B落在射线BC上的点F处,当△AEF为直角三角形时,BD的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
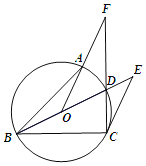
【题目】已知,如图,BD为⊙O的直径,点A、C在⊙O上并位于BD的两侧,∠ABC=45°,连结CD、OA并延长交于点F,过点C作⊙O的切线交BD延长线于点E.
(1)求证:∠F=∠ECF;
(2)当DF=6,tan∠EBC=![]() ,求AF的值.
,求AF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
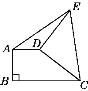
【题目】如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,将腰CD以D为中心逆时针旋转90°至DE,连接AE、CE,△ADE的面积为3,则BC的长为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
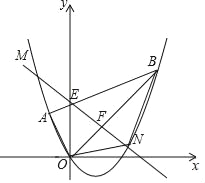
【题目】如图,平面直角坐标系xOy中点A的坐标为(﹣1,1),点B的坐标为(3,3),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点E.
(1)求点E的坐标;
(2)求抛物线的函数解析式;
(3)点F为线段OB上的一个动点(不与点O、B重合),直线EF与抛物线交于M、N两点(点N在y轴右侧),连接ON、BN,当四边形ABNO的面积最大时,求点N的坐标并求出四边形ABNO面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=BC,P为△ABC内部一点,且∠APB=∠BPC=135°
(1)求证:△PAB∽△PBC
(2)求证:PA=2PC
(3)若点P到三角形的边AB,BC,CA的距离分别为h1,h2,h3,求证h12=h2·h3

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com