
 如图,直线x⊥直线y于点O,直线x⊥AB于点B,E是线段AB上一定点,D点为线段OB上的一动点(点D不与点O、B重合),CD⊥DE交直线y于点C,连接AC,∠BED、∠DCO的角平分线的交点为P.
如图,直线x⊥直线y于点O,直线x⊥AB于点B,E是线段AB上一定点,D点为线段OB上的一动点(点D不与点O、B重合),CD⊥DE交直线y于点C,连接AC,∠BED、∠DCO的角平分线的交点为P.分析 (1)由垂直的定义和三角形的内角和得到结论;
(2)根据平行线的性质得到结论;
(3)利用外角的性质和角平分线的性质求得∠P的大小等于45°是个定值.
解答 解:(1)∵直线x⊥直线y于点O,
∴∠COD=90°,∵∠OCD=60°,
∴∠CDO=30°,
∵∠CDE=90°,
∴∠EDB=60°,
∴∠BED=30°;
(2)①CD⊥AC正确,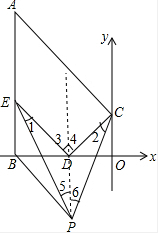
由(1)证得;∠CDO=∠BED,
∵∠CDO=∠A,
∴∠BED=∠A,
∴AC∥DE,
∵ED⊥CD,
∴AC⊥CD,
(3)如图连接PD并延长PD,∵∠5=∠3-∠1,∠6=∠4-∠2,
∴∠5+∠6=∠3+∠4-(∠1+∠2),
∵∠3+∠4=90°,∠1+∠2=$\frac{1}{2}$$∠BED+\frac{1}{2}∠DCO$
=$\frac{1}{2}$(∠BED+∠DCO)=$\frac{1}{2}$×90°=45°
∴∠5+∠6=45°,
∴∠EPC=45°是个定值.
点评 本题考查了,平行线的判定和性质,垂线的定义,三角形的内角和,辅助线的作法是关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=12cm,BC=15cm,点P从点A出发,以1cm/s的速度向点D运动,点Q从点C同时出发,以2cm/s的速度向B点运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.从运动开始,使PQ=CD,需经过多少时间?为什么?
如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=12cm,BC=15cm,点P从点A出发,以1cm/s的速度向点D运动,点Q从点C同时出发,以2cm/s的速度向B点运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.从运动开始,使PQ=CD,需经过多少时间?为什么?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com