
【题目】如图,把正六边形各边按同一方向延长,使延长的线段与原正六边形的边长相等,顺次连接这六条线段外端点可以得到一个新的正六边形,…,重复上述过程,经过2018次后,所得到的正六边形边长是原正六边形边长的( ) 
A.( ![]() )2016倍
)2016倍
B.( ![]() )2017倍
)2017倍
C.( ![]() )2018倍
)2018倍
D.( ![]() )2019倍
)2019倍
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】深圳市某学校抽样调查,A类学生骑共享单车,B类学生坐公交车、私家车等,C类学生步行,D类学生(其它),根据调查结果绘制了不完整的统计图.
类型 | 频数 | 频率 |
A | 30 |
|
B | 18 | 0.15 |
C |
| 0.40 |
D |
|
|
(1)学生共人, ![]() ,
, ![]() ;
;
(2)补全条形统计图;
(3)若该校共有2000人,骑共享单车的有人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,点P从点B出发,沿BC向点C匀速运动,速度为1cm/s;过点P作PD∥AB,交AC于点D,同时,点Q从点A出发,沿AB向点B匀速运动,速度为2cm/s;当一个点停止运动时,另一个点也停止运动,连接PQ.设运动时间为t(s)(0<t<2.5),解答下列问题:
(1)当t为何值时,四边形ADPQ为平行四边形?
(2)设四边形ADPQ的面积为y(cm2),试确定y与t的函数关系式;
(3)在运动过程中,是否存在某一时刻t,使S四边形ADPQ:S△PQB=13:2?若存在,请说明理由,若存在,求出t的值,并求出此时PQ的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
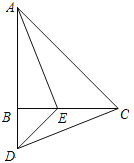
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC.
① 求证:△ABE≌△CBD;
② 若∠CAE=30°,求∠BDC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个隧道的横断面,它的形状是以点O为圆心的圆的一部分,如果圆的半径为 ![]() m,弦CD=4m,那么隧道的最高处到CD的距离是( )
m,弦CD=4m,那么隧道的最高处到CD的距离是( ) 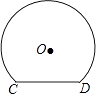
A.![]() m
m
B.4m
C.![]() m
m
D.6m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a>b,请用“>”或“<”填空:
(1)a-1________b-1;(2)![]() a________
a________![]() b;(3)a+c________b+c;(4)-3a________-3b;(5)-
b;(3)a+c________b+c;(4)-3a________-3b;(5)-![]() a-c________-
a-c________-![]() b-c.
b-c.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了对学生进行爱国主义教育,某校组织学生去看演出,有甲乙两种票,已知甲乙两种票的单价比为4:3,单价和为42元.
(1)甲乙两种票的单价分别是多少元?
(2)学校计划拿出不超过750元的资金,让七年级一班的36名学生首先观看,且规定购买甲种票必须多于15张,有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为_____秒时,△ABP和△DCE全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AC=BC,CD=CE,∠ACB=∠DCE=α,AD、BE相交于点M,连接CM.
(1)求证:BE=AD;并用含α的式子表示∠AMB的度数;
(2)当α=90°时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图2,判断△CPQ的形状,并加以证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com