
【题目】如图,在平面直角坐标系xOy中,拋物线y=﹣ ![]() x2
x2 ![]() x与x轴交于O,A,点B在抛物线上且横坐标为2.
x与x轴交于O,A,点B在抛物线上且横坐标为2.
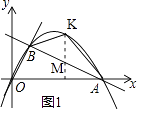
(1)如图1,△AOB的面积是多少?
(2)如图1,在线段AB上方的抛物线上有一点K,当△ABK的面积最大时,求点K的坐标及△ABK的面积;
(3)在(2)的条件下,点H 在y轴上运动,点I在x轴上运动.则当四边形BHIK周长最小时,求出H、I的坐标以及四边形BHIK周长的最小值.
【答案】
(1)解:当y=0时,得A(10,0);
当x=2时,y=4,所以B(2,4),
∴ ![]() ;
;
(2)解:过K作KM⊥x轴交AB于M点,
设K(m,﹣ ![]() m2
m2 ![]() m),(2<m<10),
m),(2<m<10),
∵A(10,0),B(2,4),
∴直线AB的解析式为y=﹣ ![]() x+5,
x+5,
则KM=﹣ ![]() m2
m2 ![]() m﹣(﹣
m﹣(﹣ ![]() m+5)=﹣
m+5)=﹣ ![]() m2+3m﹣5,
m2+3m﹣5,
∴S△ABK= ![]() KM|xA﹣xB|=4KM=﹣m2+12m﹣20=﹣(m﹣6)2+16,
KM|xA﹣xB|=4KM=﹣m2+12m﹣20=﹣(m﹣6)2+16,
∴当m=6时,S△ABK有最大值.
此时,K(6,6),S△ABK=16.
(3)解:如图,作点B关于y轴的对称点B′(﹣2,4)、点K关于x轴的对称点K′(6,﹣6),
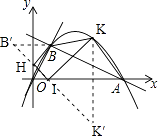
连接B′K′,分别交x轴于点I,交y轴于点H,此时四边形BHIK的周长最小,
∴B′K′的解析式为y=﹣ ![]() x+
x+ ![]() ,
,
∴H(0, ![]() )、I(
)、I( ![]() ,0),
,0),
∴四边形BHIK周长的最小值为B′K′+BK= ![]() +
+ ![]() =2
=2 ![]() +2
+2 ![]() .
.
【解析】(1)要求面积可求高,即yB;(2)(三边均没有水平边或竖直边的三角形可称为斜三角形)△ABK是斜三角形,须过点K做x轴的垂线,把它分割为两个有竖直边的三角形,设出自变量,构建函数,解决最值问题;(3)四边形BHIK周长可转化为多条线段的和,可利用对称法求两线段之和最小,即做出定点B、K分别关于y、x轴的对称点,当三条线段B'H,HI、IK' 在一条直线上时,周长最短..
【考点精析】利用轴对称-最短路线问题对题目进行判断即可得到答案,需要熟知已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径.


科目:初中数学 来源: 题型:
【题目】某文具零售店准备从批发市场选购A、B两种文具,批发价A种为12元/件,B种为8元/件.若该店零售A、B两种文具的日销售量y(件)与零售价x(元/件)均成一次函数关系.(如图) 
(1)求y与x的函数关系式;
(2)该店计划这次选购A、B两种文具的数量共100件,所花资金不超过1000元,并希望全部售完获利不低于296元,若按A种文具每件可获利4元和B种文具每件可获利2元计算,则该店这次有哪几种进货方案?
(3)若A种文具的零售价比B种文具的零售价高2元/件,求两种文具每天的销售利润W(元)与A种文具零售价x(元/件)之间的函数关系式,并说明A、B两种文具零售价分别为多少时,每天销售的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直角坐标平面内两点A(-2,-3)、B(3,-3),将点B向上平移5个单位到达点C,求:

(1)A、B两点间的距离;
(2)写出点C的坐标;
(3)四边形OABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图放置的△OAB1 , △B1A1B2 , △B2A2B3 , …都是边长为2的等边三角形,点A在y轴上,点O,B1 , B2 , B3…都在直线l上,则点B2017的坐标是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将△ABC的∠C折起,翻折后角的顶点位置记作C′,当C′落在AC上时(如图1),易证:∠1=2∠2.
当C′点落在CA和CB之间(如图2)时,或当C′落在CB、CA的同旁(如图3)时,∠1、∠2、∠3关系又如何?请写出你的猜想,并就其中一种情况给出证明.



图1 图2 图3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD与AB,CD交于A,D两点,EC,BF与AB,CD交于E,C,B,F,且∠1=∠2,∠B=∠C,

(1)说明CE∥BF.
(2)你能得出∠B=∠3和∠A=∠D这两个结论吗?若能,写出你得出结论的过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填写理由:
已知:如图,ABC是直线,∠1=115°,∠D=65°.
求证:AB∥DE.

证明:∵ABC是一直线,(已知)
∴∠1+∠2=180°( )
∵∠1=115°(已知)
∴∠2=65°
又∵∠D=65°(已知)
∴∠2=∠D
∴ ∥ ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴相交于A、B两点,点B的坐标为(3,0),与y轴相交于点C(0,﹣3),顶点为D.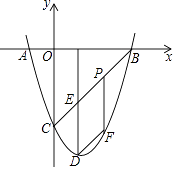
(1)求出抛物线y=x2+bx+c的表达式;
(2)连结BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作PF∥DE交抛物线于点F,设点P的横坐标为m.
①当m为何值时,四边形PEDF为平行四边形.
②设四边形OBFC的面积为S,求S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(0,a),B(b,a),且a,b满足(a﹣3)2+|b﹣6|=0,现同时将点A,B分别向下平移3个单位,再向左平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB.

(1)求点C,D的坐标及四边形ABDC的面积S四边形ABCD;
(2)在y轴上是否存在一点M,连接MC,MD,使S△MCD=![]() S四边形ABCD?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
S四边形ABCD?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
(3)点P是直线BD上的一个动点,连接PA,PO,当点P在BD上移动时(不与B,D重合),直接写出∠BAP,∠DOP,∠APO之间满足的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com