
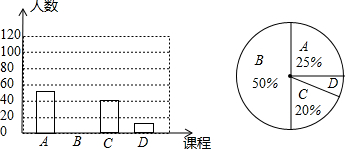
分析 (1)根据喜欢京剧的人数和所占的百分比即可求出总人数;
(2)用总人数乘以喜欢武术人数所占的百分比,求出喜欢武术的人数,从而补全统计图;
(3)用该校的总人数乘以喜欢国画的人数所占的百分比即可得出答案.
解答 解:(1)根据题意得:
40÷20%=200(人).
答:共调查了200名学生.
(2)喜欢武术的学生有:200×50%=100(人),补图如下: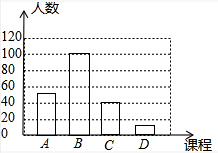
(3)根据题意得:
1200×(1-50%-25%-20%)=60(人).
该校学生最喜欢国画的约有60人.
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.


科目:初中数学 来源: 题型:选择题
| A. | 1名 | B. | 2名 | C. | 3名 | D. | 4名 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在以点O为原点的直角坐标系中,一次函数y=-$\frac{1}{2}$x+1的图象与x轴交于A,与y轴交于点B,点C在第二象限内且为直线AB上一点,OC=$\frac{1}{2}$AB,反比例函数y=$\frac{k}{x}$的图象经过点C,则k的值为-$\frac{11}{50}$.
如图,在以点O为原点的直角坐标系中,一次函数y=-$\frac{1}{2}$x+1的图象与x轴交于A,与y轴交于点B,点C在第二象限内且为直线AB上一点,OC=$\frac{1}{2}$AB,反比例函数y=$\frac{k}{x}$的图象经过点C,则k的值为-$\frac{11}{50}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,已知点A(2,3)、B(6,3),连结AB.若对于平面内一点P,线段AB上都存在点Q,使得PQ≤1,则称点P是线段AB的“邻近点”.
如图,在平面直角坐标系中,已知点A(2,3)、B(6,3),连结AB.若对于平面内一点P,线段AB上都存在点Q,使得PQ≤1,则称点P是线段AB的“邻近点”.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com