
 ≈1.732)
≈1.732)
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:
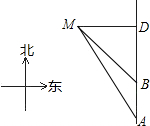 如图,一艘货轮向正北方向航行,在点A处测得灯塔M在北偏西30°,货轮以每小时20海里的速度航行,1小时后到达B处,测得灯塔M在北偏西45°,问该货轮到达灯塔正东方向D处时,货轮与灯塔M的距离是多少?
如图,一艘货轮向正北方向航行,在点A处测得灯塔M在北偏西30°,货轮以每小时20海里的速度航行,1小时后到达B处,测得灯塔M在北偏西45°,问该货轮到达灯塔正东方向D处时,货轮与灯塔M的距离是多少?| 3 |
查看答案和解析>>
科目:初中数学 来源:第1章《解直角三角形》中考题集(44):1.3 解直角三角形(解析版) 题型:解答题
 ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源:第21章《解直角三角形》中考题集(41):21.5 应用举例(解析版) 题型:解答题
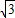 ≈1.732)
≈1.732)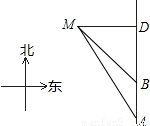
查看答案和解析>>
科目:初中数学 来源:第25章《解直角三角形》中考题集(39):25.3 解直角三角形及其应用(解析版) 题型:解答题
 ≈1.732)
≈1.732)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com