
(1)观察与发现:将矩形纸片AOCB折叠,使点C与点A重合,点B落在点B′处(如图),折痕为EF.小明发现△AEF为等腰三角形,你同意吗?请说明理由.
(2)实践与应用:以点O为坐标原点,分别以矩形的边OC、OA为x轴、y轴建立如图所示的直角坐标系,若顶点B的坐标为(9,3),请求出折痕EF的长及EF所在直线的函数关系式.
(1)同意,理由见解析;(2) ,y=3x-12.
,y=3x-12.
解析试题分析:(1)同意.
理由:因为AB∥OC,所以∠AEF=∠EFC.根据折叠性质,有∠AFE=∠EFC.所以∠AEF=∠AFE,AE=AF.△AEF为等腰三角形.
(2)过点E作EG⊥OC于点G.设OF=x,则CF=9-x;由折叠可知:AF=9-x.
在Rt△AOF中,AF2=AO2+OF2即:32+x2=(9-x)2,解得x=4,AE=AF=9-x=5,FG=OG-OF=5-4=1.在Rt△EFG中,EF2=EG2+FG2=10,求出EF=
设直线EF的解析式为y=kx+b(k≠0),因为点E(5,3)和点F(4,0)在直线EF上,所以,代入解得解得k,b,进而求出解析式.
试题解析:(1)同意.
理由:∵AB∥OC,∴∠AEF=∠EFC.
根据折叠性质,有∠AFE=∠EFC.
∴∠AEF=∠AFE,
∴AE=AF.
∴△AEF为等腰三角形.
(2)过点E作EG⊥OC于点G.
设OF=x,则CF=9-x;
由折叠可知:AF=9-x.
在Rt△AOF中,AF2=AO2+OF2
∴32+x2=(9-x)2,
∴x=4,9-x=5.
∴AE=AF=5,
∴FG=OG-OF=5-4=1.
在Rt△EFG中,
EF2=EG2+FG2=10,
∴EF=
设直线EF的解析式为y=kx+b(k≠0),
∵点E(5,3)和点F(4,0)在直线EF上,
∴3=5k+b,0=4k+b,
解得:k=3,b=-12.
∴y=3x-12.
考点:1.折叠问题.2.一次函数的解析式.3.勾股定理.


科目:初中数学 来源: 题型:解答题
某文具店准备购进甲,乙两种钢笔,若购进甲种钢笔100支,乙种钢笔50支,需要1000元,若购进甲种钢笔50支,乙种钢笔30支,需要550元.
(1)求购进甲,乙两种钢笔每支各需多少元?
(2)若该文具店准备拿出1000元全部用来购进这两种钢笔,考虑顾客需求,要求购进甲中钢笔的数量不少于乙种钢笔数量的6倍,且不超过乙种钢笔数量的8倍,那么该文具店共有几种进货方案?
(3)若该文具店销售每支甲种钢笔可获利润2元,销售每支乙种钢笔可获利润3元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某工厂现有甲种原料360kg,乙种原料290kg,计划用它们生产A、B两种产品共50件,已知每生产一件A种产品,需要甲种原料9kg、乙种原料3kg,获利700元,生产一件B种产品,需要甲种原料4kg、乙种原料10kg,可获利1200元.
(1)利用这些原料,生产A、B两种产品,有哪几种不同的方案?
(2)设生产两种产品总利润为y(元),其中生产A中产品x(件),试写出y与x之间的函数解析式.
(3)利用函数性质说明,采用(1)中哪种生产方案所获总利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知直线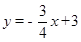 与x轴、y轴分别交于点A、B,线段AB为直角边在第一象限内作等腰Rt△ABC,∠BAC=90°.
与x轴、y轴分别交于点A、B,线段AB为直角边在第一象限内作等腰Rt△ABC,∠BAC=90°.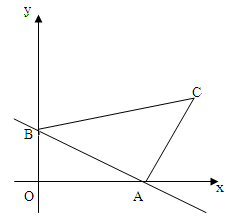
(1)求△AOB的面积;
(2)求点C坐标;
(3)点P是x轴上的一个动点,设P(x,0)
①请用x的代数式表示PB2、PC2;
②是否存在这样的点P,使得|PC-PB|的值最大?如果不存在,请说明理由;
如果存在,请求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
一次函数y=kx+4的图象经过点(-3,-2),则
(1)求这个函数表达式;并画出该函数的图象.
(2)判断(-5,3)是否在此函数的图象上;
(3)求把这条直线沿x轴向右平移1个单位长度后的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
国家推行“节能减排,低碳经济”的政策后,某企业推出一种叫“CNG”的改烧汽油为天然气的装置,每辆车改装费为b元.据市场调查知:每辆车改装前、后的燃料费(含改装费) 、
、 (单位:元)与正常运营时间
(单位:元)与正常运营时间 (单位:天)之间分别满足关系式:
(单位:天)之间分别满足关系式: 、
、 ,如图所示.
,如图所示.
试根据图像解决下列问题:
(1)每辆车改装前每天的燃料费 = 元,每辆车的改装费b= 元.正常运营 天后,就可以从节省燃料费中收回改装成本.
= 元,每辆车的改装费b= 元.正常运营 天后,就可以从节省燃料费中收回改装成本.
(2)某出租汽车公司一次性改装了100辆车,因而,正常运营多少天后共节省燃料费40万元?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,一次函数 与反比例函数
与反比例函数 的图象相交于点A,且点A的纵坐标为1.
的图象相交于点A,且点A的纵坐标为1.
(1)求反比例函数的解析式;
(2)根据图象写出当x>0时,一次函数的值大于反比例函数的值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
阅读材料:若a,b都是非负实数,则 .当且仅当a=b时,“=”成立.
.当且仅当a=b时,“=”成立.
证明:∵ ,∴
,∴ .
.
∴ .当且仅当a=b时,“=”成立.
.当且仅当a=b时,“=”成立.
举例应用:已知x>0,求函数 的最小值.
的最小值.
解: .当且仅当
.当且仅当 ,即x=1时,“=”成立.
,即x=1时,“=”成立.
当x=1时,函数取得最小值,y最小=4.
问题解决:汽车的经济时速是指汽车最省油的行驶速度.某种汽车在每小时70~110公里之间行驶时(含70公里和110公里),每公里耗油 升.若该汽车以每小时x公里的速度匀速行驶,1小时的耗油量为y升.
升.若该汽车以每小时x公里的速度匀速行驶,1小时的耗油量为y升.
(1)求y关于x的函数关系式(写出自变量x的取值范围);
(2)求该汽车的经济时速及经济时速的百公里耗油量(结果保留小数点后一位).
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
为了落实党中央提出的“惠民政策”,我市今年计划开发建设A、B两种户型的“廉租房”共40套.投入资金不超过200万元,又不低于198万元.开发建设办公室预算:一套A型“廉租房”的造价为5.2万元,一套B型“廉租房”的造价为4.8万元.
(1)请问有几种开发建设方案?
(2)哪种建设方案投入资金最少?最少资金是多少万元?
(3)在(2)的方案下,为了让更多的人享受到“惠民”政策,开发建设办公室决定通过缩小“廉租房”的面积来降低造价、节省资金.每套A户型“廉租房”的造价降低0.7万元,每套B户型“廉租房”的造价降低0.3万元,将节省下来的资金全部用于再次开发建设缩小面积后的“廉租房”,如果同时建设A、B两种户型,请你直接写出再次开发建设的方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com