
【题目】如图,已知菱形ABCD的对角线AC,BD相交于点O,延长AB至点E,使BE=AB,连接CE.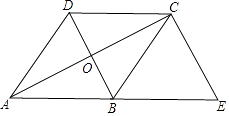
(1)求证:四边形BECD是平行四边形;
(2)若∠E=60°,AC=4 ![]() ,求菱形ABCD的面积.
,求菱形ABCD的面积.
【答案】
(1)证明:∵四边形ABCD是菱形,
∴AB=CD,AB∥CD,
又∵BE=AB,
∴BE=CD,BE∥CD,
∴四边形BECD是平行四边形
(2)解:∵四边形BECD是平行四边形,
∴DB∥CE,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠E=∠OBA,
∴AC⊥CE.
在直角△ACE中,∵∠E=60°,AC=4 ![]() ,
,
∴CE= ![]() =
= ![]() =4.
=4.
∵四边形BECD是平行四边形,
∴BD=CE=4,
∴S菱形ABCD= ![]() ACBD=
ACBD= ![]() ×4
×4 ![]() ×4=8
×4=8 ![]() .
.
【解析】(1)由菱形的性质得AB=CD,AB∥CD,又用等量代换得出BE=CD,BE∥CD,根据平行四边形的判定定理得出结论;(2)由平行四边形的性质得DB∥CE,由菱形的性质得AC⊥BD,进而 根据平行线的性质得出∠E=∠OBA,AC⊥CE.解直角三角形得CE的长度,最后根据平行四边形的性质及菱形面积公式得出结论。


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.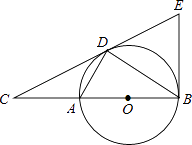
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6, ![]() .求BE的长.
.求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个长为![]() ,宽为
,宽为![]() 的长方形,沿图中虚线用剪刀均匀分成四块小长方形,然后按图2形状拼成一个正方形.
的长方形,沿图中虚线用剪刀均匀分成四块小长方形,然后按图2形状拼成一个正方形.
(1)请用两种不同方法,求图2中阴影部分的面积(不用化简)
方法1:____________________
方法2:____________________
(2)观察图2,写出![]() ,
,![]() ,
,![]() 之间的等量关系,并验证;
之间的等量关系,并验证;

(3)根据(2)题中的等量关系,解决如下问题:
①若![]() ,
,![]() ,求
,求![]() 的值;
的值;
②若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年12月,旗团委号召各校组织开展捐赠衣物的“暖冬行动”![]() 某校七年级六个班参加了这次捐赠活动,若每班捐赠衣物以100件为基准,超过的件数用正数表示,不足的件数用负数表示,记录如下:
某校七年级六个班参加了这次捐赠活动,若每班捐赠衣物以100件为基准,超过的件数用正数表示,不足的件数用负数表示,记录如下:
班级 | 一班 | 二班 | 三班 | 四班 | 五班 | 六班 |
人数 | 40 | 43 | 45 | 44 | 40 | 38 |
件数 |
|
|
|
|
|
|
![]() 捐赠衣物最多的班比最少的班多多少件?
捐赠衣物最多的班比最少的班多多少件?
![]() 该校七年级学生共捐赠多少件衣物?该校七年级学生平均每人捐赠多少件衣物?
该校七年级学生共捐赠多少件衣物?该校七年级学生平均每人捐赠多少件衣物?
查看答案和解析>>
科目:初中数学 来源: 题型:
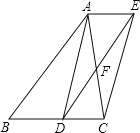
【题目】如图,已知点D是△ABC的边BC的中点,直线AE∥BC,过点D作直线DE∥AB,分别交AE、AC于点E、F。
(1)求证:四边形ADCE是平行四边形;
(2)如果四边形ADCE是矩形,△ABC应满足什么条件?并说明理由;
(3)如果四边形ADCE是菱形,直接写出△ABC应满足的条件是 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,池塘边有一块长为18m,宽为10m的长方形土地,现在将其 余三面留出宽都是xm的小路,中间余下的长方形部分做菜地,用整式表示:
(1)菜地的长a= m,宽b= m;
(2)菜地面积S= m2;
(3)当x=0.5m时,菜地面积是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com