
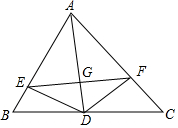
 如图所示,AD是∠BAC的平分线,DE⊥AB,DF⊥AC,垂足分别为E,F,连接EF,EF与AD交于点G,求证:AD垂直平分EF.
如图所示,AD是∠BAC的平分线,DE⊥AB,DF⊥AC,垂足分别为E,F,连接EF,EF与AD交于点G,求证:AD垂直平分EF. 分析 求出DE=DF,∠AED=∠AFD=90°,根据HL证Rt△AED≌Rt△AFD,推出AE=AF,根据等腰三角形性质推出即可.
解答 证:∵AD是∠BAC的平分线,
DE⊥AB,DF⊥AC,
∴DE=DF,∠AED=∠AFD=90°,
在Rt△AED和Rt△AFD中
$\left\{\begin{array}{l}{AD=AD}\\{DE=DF}\end{array}\right.$,
∴Rt△AED≌Rt△AFD(HL),
∴AE=AF,
∵AD是∠BAC的平分线,
∴AD垂直平分EF.
点评 本题考查了全等三角形的性质和判定和等腰三角形的性质的应用,注意:①全等三角形的对应边相等,对应角相等,②全等三角形的判定定理有SAS,ASA,AAS,SSS,③等腰三角形的顶角的平分线平分底边,并且垂直于底边.


科目:初中数学 来源: 题型:解答题
| 时刻 | 8时 | 10时 | 12时 | 14时 | 16时 | 18时 |
| 体温 | 38.5 | 39.5 | 38 | |||
| 与正常人的正 常体温的差值 | +1.8 | +2.6 | +0.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 流花河的警戒水位是33.5米,表记录的是今年某一周内的水位变化情况,取河流的警戒水位作为0点,并且上周末(星期六)的水位达到警戒水位,(正号表示水位比前一天上升,负号表示水位比前一天下降.)
流花河的警戒水位是33.5米,表记录的是今年某一周内的水位变化情况,取河流的警戒水位作为0点,并且上周末(星期六)的水位达到警戒水位,(正号表示水位比前一天上升,负号表示水位比前一天下降.)| 星期 | 日 | 一 | 二 | 三 | 四 | 五 | 六 |
| 水位变化 (米) | +0.3 | +0.81 | -0.32 | +0.04 | +0.27 | -0.35 | -0.02 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x4+4x4y-2x3 | B. | -πx4-3x2+x | C. | -x4+5y3+xy-2 | D. | $\frac{3{x}^{4}-1}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com