
【题目】从﹣3,﹣2,﹣1,0,1,3,4这七个数中随机抽取一个数记为a,a的值既是不等式组 ![]() 的解,又在函数y=
的解,又在函数y= ![]() 的自变量取值范围内的概率是 .
的自变量取值范围内的概率是 .
科目:初中数学 来源: 题型:
【题目】如图,在所给正方形网格(每个小网格的边长是1)图中完成下列各题.
(1)格点△ABC(顶点均在格点上)的面积=_________;

(2)画出格点△ABC关于直线DE对称的△A1B1C1;
(3)在DE上画出点P,使PB+PC最小,并求出这个最小值.
【答案】(1)面积等于5(2)图形见解析(3)最小值是根号17
【解析】试题分析:(1)利用勾股定理求出三角形边长,并证明是直角三角形求面积.(2)画出A,B,C的对称点A1,B2,C3,连接三角形.(3)利用对称利用两点之间直线最短求最小值.
试题解析:
(1)分别利用勾股定理求得AC=2![]() ,AB=
,AB=![]() ,BC=
,BC=![]() ,
, ![]() ,所以∠ACB=90°,面积等于
,所以∠ACB=90°,面积等于![]() =5.
=5.
(2)画出A,B,C的对称点A1,B2,C3,连接三角形.如下图.

(3)作B点对称B’,连接B’C交DE于P,B’P+PC=BP+CP,所以使PB+PC最小.
利用勾股定理B’C=![]() ,
,
所以最小值是根号17.

点睛:平面上最短路径问题
(1)归于“两点之间的连线中,线段最短”.凡属于求“变动的两线段之和的最小值”时,大都应用这一模型.
(2)归于“三角形两边之差小于第三边”.凡属于求“变动的两线段之差的最大值”时,大都应用这一模型.
(3)平面图形中,直线同侧两点到直线上一点距离之和最短问题.

【题型】解答题
【结束】
23
【题目】已知一次函数y=kx+7的图像经过点A(2,3).
(1)求k的值;
(2)判断点B(-1,8),C(3,1)是否在这个函数的图像上,并说明理由;
(3)当-3<x<-1时,求y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组: ![]() .请结合题意填空,完成本体的解法.
.请结合题意填空,完成本体的解法.
![]()
(1)解不等式(1),得________;
(2)解不等式(2),得________;
(3)把不等式 (1)和 (2)的解集在数轴上表示出来.
(4)原不等式的解集为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平行于y轴的动直线a的表达式为x=t,直线b的表达式为y=x,直线c的表达式为y=﹣![]() x+2,且动直线a分别交直线b、c于点D、E(E在D的上方),P是y轴上一个动点,且满足△PDE是等腰直角三角形,则点P的坐标是________.
x+2,且动直线a分别交直线b、c于点D、E(E在D的上方),P是y轴上一个动点,且满足△PDE是等腰直角三角形,则点P的坐标是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明:
已知:如图,四边形ABCD中,∠A=106°![]() , ∠ABC=74°
, ∠ABC=74°![]() ,BD⊥DC于点D, EF⊥DC于点F.
,BD⊥DC于点D, EF⊥DC于点F.
求证:∠1=∠2.

证明: ∵∠A=106°![]() ,∠ABC=74°
,∠ABC=74°![]() (已知)
(已知)
∴∠A+∠ABC=180°
![]() ( )
( )
∴∠1=
∵BD⊥DC,EF⊥DC (已知)
∴∠BDF=∠EFC=90°( )
∴BD∥ ( )
∴∠2= ( )
![]() (已证)
(已证)
∴∠1=∠2 ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.若AE=1,则FM的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,任意一点P(a,b)经平移后对应点P1(a﹣2,b+3),将△ABC作同样的平移得到△A1B1C1.
(1)求A1,B1,C1的坐标;
(2)指出这一平移的平移方向和平移距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】麻城市思源实验学校自从开展“高效课堂”模式以来,在课堂上进行当堂检测效果很好.每节课40分钟教学,假设老师用于精讲的时间x(单位:分钟)与学生学习收益量y的关系如图1所示,学生用于当堂检测的时间x(单位:分钟)与学生学习收益y的关系如图2所示(其中OA是抛物线的一部分,A为抛物线的顶点),且用于当堂检测的时间不超过用于精讲的时间. 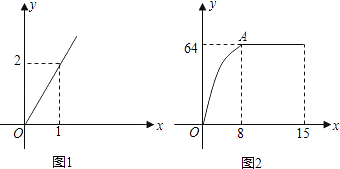
(1)求老师精讲时的学生学习收益量y与用于精讲的时间x之间的函数关系式;
(2)求学生当堂检测的学习收益量y与用于当堂检测的时间x的函数关系式;
(3)问此“高效课堂”模式如何分配精讲和当堂检测的时间,才能使学生在这40分钟的学习收益总量最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末小明和同学们去“绿博园”的枫湖坐船,观赏风景;如图,小明正在A处的小船上,B处小船上的游客发现点A在点B的正西方向上,C处小船上的游客发现点A在点C的南偏东30°方向上,已知点C在点B的北偏西60°方向上,且B、C两地相距120米.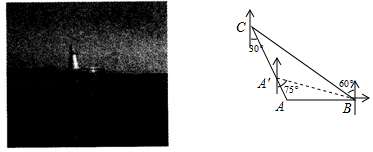
(1)求出此时点A到点C的距离;
(2)若小明从A处沿AC方向向C驶去,当到达点A′时,测得点B在A′的南偏东75°的方向上,求此时小明所乘坐的小船走的距离.(注:结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com