
【题目】菱形ABCD的边长为3,∠BAD=60°.
(1)连接AC,过点D作DE⊥AB于点E,DF⊥BC交AC于点F,DE、DF于点M、N.
①依题意补全图1;
②求MN的长;
(2)如图2,将(1)中∠EDF以点D为中心,顺时针旋转45°,其两边DE′、DF′分别与直线AB、BC相交于点Q、P,连接QP,请写出求△DPQ的面积的思路.(可以不写出计算结果)

【答案】(1)①答案见解析;②![]() ;(2)答案见解析.
;(2)答案见解析.
【解析】
(1)①根据条件画出图形即可;②连接BD,利用菱形的性质得出△ABD为等边三角形,再利用勾股定理和平行线的性质得出结果即可;(3)由勾股定理和三角形相似的判定及三角形的面积公式求出结果即可.
本题解析:
(1)②证明:连接BD,设BD交AC于O.
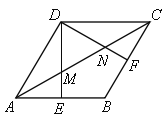
∵在菱形ABCD中,∠DAB=60°,AD=AB,∴△ABD为等边三角形,AC⊥BD于点O,∠DAC=![]() ∠DAB=30°,∴OD=
∠DAB=30°,∴OD=![]() AD=
AD=![]() .
.
在Rt△AOD中,OA=![]() =
=![]() ,∴AC=2OA=
,∴AC=2OA=![]() .
.
∵DE⊥AB,∴E为AB中点,∵AE∥CD,∴![]() ,同理:
,同理:![]() ,∴M、N是线段AC的三等分点,∴MN=
,∴M、N是线段AC的三等分点,∴MN=![]() AC=
AC=![]() .
.
(2)解:
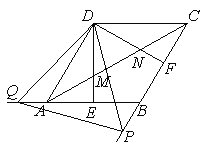
a.在Rt△DCF中,先求出DF的长;
b.在Rt△DFP中,求出DP的长;
c.通过证明△DQA≌△DPB,证明△DPQ是等边三角形;
d.根据DP的长,计算等边三角形的面积.


科目:初中数学 来源: 题型:
【题目】如图,已知平行四边形ABCD,延长AD到E,使DE=AD,连接BE与DC交于O点.

(1)求证:△BOC≌△EOD;
(2)当△ABE满足什么条件时,四边形BCED是菱形?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点C1在边BC上,将△C1CD绕点D顺时针旋转90°得到△A1AD.A1F平分∠BA1C1,交BD于点F,过点F作FE⊥A1C1,垂足为E,当A1E=3,C1E=2时,则BD的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高3米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有27米的距离(B,F,C在一条直线上).

(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.
(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
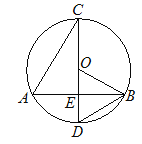
【题目】如图,CD为⊙O的直径,弦AB交CD于点E,连接BD、OB.
(1)求证:△AEC∽△DEB;
(2)若CD⊥AB,AB=8,DE=2,求⊙O的半径.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知P(﹣3,m)和 Q(1,m)是抛物线y=x2+bx﹣3上的两点.

(1)求b的值;
(2)将抛物线y=x2+bx﹣3的图象向上平移k(是正整数)个单位,使平移后的图象与x轴无交点,求k的最小值;
(3)将抛物线y=x2+bx﹣3的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合新图象回答:当直线y=x+n与这个新图象有两个公共点时,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某加工厂以每吨3000元的价格购进50吨原料进行加工.若进行粗加工,每吨加工费用为600元,需![]() 天,每吨售价4000元;若进行精加工,每吨加工费用为900元,需
天,每吨售价4000元;若进行精加工,每吨加工费用为900元,需![]() 天,每吨售价4500元.现将这50吨原料全部加工完.设其中粗加工x吨,获利y元.
天,每吨售价4500元.现将这50吨原料全部加工完.设其中粗加工x吨,获利y元.
(1)请完成表格并求出y与x的函数关系式(不要求写自变量的范围);

(2)如果必须在20天内完成,如何安排生产才能获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C为⊙O上一点,AD⊥CD,(点D在⊙O外)AC平分∠BAD.
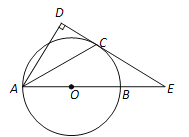
(1)求证:CD是⊙O的切线;
(2)若DC、AB的延长线相交于点E,且DE=12,AD=9,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过对下面数学模型的研究学习,解决下列问题:
(模型呈现)(1)如图1,![]() ,
,![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .由
.由![]() ,得
,得![]() .又
.又![]() ,可以推理得到
,可以推理得到![]() .进而得到
.进而得到![]() ,
,![]() .我们把这个数学模型称为“
.我们把这个数学模型称为“![]() 字”模型或“一线三等角”模型;
字”模型或“一线三等角”模型;

(模型应用)(2)①如图2,![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,且
,且![]() 于点
于点![]() ,
,![]() 与直线
与直线![]() 交于点
交于点![]() 是
是![]() 的中点;
的中点;

②如图3,在平面直角坐标系![]() 中,点
中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 为平面内任一点.若
为平面内任一点.若![]() 是以
是以![]() 为斜边的等腰直角三角形,请直接写出点
为斜边的等腰直角三角形,请直接写出点![]() 的坐标.
的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com