Question

18．已知抛物线y=ax²-x+b的图象过点A（3，-6），且交x轴于点B（1，0）和点C，顶点为D．
（1）求这条抛物线的解析式，并画出草图；
（2）在线段OC上有一点P，满足∠PDC=∠BAC，求点P的坐标；
（3）在x轴上是否存在一点M，使以点M为圆心的⊙M与AC、DC所在的直线及y轴都相切？如果存在请求出点M的坐标，若不存在请说明理由．

Answer 1

分析 （1）把点A、B两点坐标代入y=ax²-x+b，解方程组即可．
（2）如图1中，作AM⊥x轴于M，对称轴与x轴交于点N．只要证明△CDP∽△CAB，可得$\frac{CP}{CB}$=$\frac{CD}{AC}$，由此解决问题．
（3）如图2中，设点M坐标为（m，0）．在Rt△CEM中，由CE²+EM²=CM²，列出方程即可解决问题．

解答 解：（1）∵抛物线y=ax²-x+b的图象过点A（3，-6），点B（1，0），
∴$\left\{\begin{array}{l}{a-1+b=0}\\{9a-3+b=-6}\end{array}\right.$，解得$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=\frac{3}{2}}\end{array}\right.$，
∴抛物线的解析式为y=-$\frac{1}{2}$x²-x+$\frac{3}{2}$．

（2）如图1中，作AM⊥x轴于M，对称轴与x轴交于点N．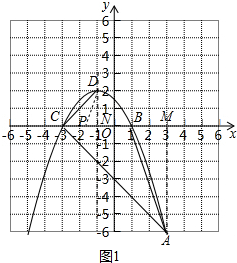

∵抛物线与x的交点坐标为B（-3，0），C（1，0），顶点D（-1，2），A（-3，6），
∴CN=DN=2，AM=CM=6，
∴△DCN，△ACM都是等腰直角三角形，
∴∠DCN=∠ACM=45°，CD=2$\sqrt{2}$，AC=6$\sqrt{2}$，
∵∠CDP=∠CAB，
∴△CDP∽△CAB，
∴$\frac{CP}{CB}$=$\frac{CD}{AC}$，
∴$\frac{CP}{4}$=$\frac{2\sqrt{2}}{6\sqrt{2}}$，
∴CP=$\frac{4}{3}$，
∴点P坐标（-$\frac{4}{3}$，0）．

（3）如图2中，设点M坐标为（m，0）．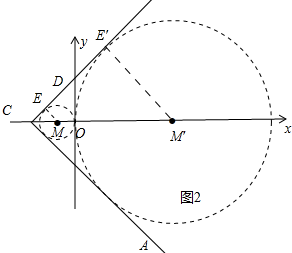

∵⊙M与CD、AC、y轴相切，设⊙M与CD相切的切点为E，
∴ME⊥CD，∵∠ECM=45°，
∴CE=EM=OM，
在Rt△CEM中，∵CE²+EM²=CM²，
∴m²+m²=（m-3）²，
整理得到，m²-6m-9=0，
∴m=3±3$\sqrt{2}$，
∴点M的坐标（3-3$\sqrt{3}$，0），（3+3$\sqrt{3}$，0）．

点评 本题考查二次函数综合题、等腰直角三角形的判定和性质、圆、切线的性质、相似三角形的判定和性质等知识，解题的关键是灵活应用这些知识解决问题，学会添加常用辅助线，学会用构建方程的思想思考问题，属于中考压轴题．