
【题目】如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.
(1)求证:∠BDC=∠A;
(2)若CE=2,DE=1,求AD的长.
【答案】
(1)证明:

连接OD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠A+∠DBO=90°,
∵CD切⊙O于D,
∴∠CDO=90°,
∴∠BDC+∠ODB=90°,
∵OD=OB,
∴∠DBO=∠ODB,
∴∠BDC=∠A
(2)解:∵CE⊥AE,
∴∠E=∠ADB=90°,
∴DB∥EC,
∴∠DCE=∠BDC,
∵∠BDC=∠A,
∴∠A=∠DCE,
∵∠E=∠E,
∴△AEC∽△CED,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴AE=4,
∴AD=AE﹣DE=4﹣1=3
【解析】(1)出现切线时,常用的辅助线为连接切点和圆心,构造直角,利用余角的性质可证出;(2)利用直径的性质和平行的性质,可证出△AEC∽△CED,对应边成比例求出AE,减去DE,求出AD.
【考点精析】关于本题考查的圆周角定理和切线的性质定理,需要了解顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能得出正确答案.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
【题目】如图,平面内的直线有相交和平行两种位置关系.
(1)如图(a),已知AB∥CD,求证:∠BPD=∠B+∠D.
(2)如图(b),已知AB∥CD,求证:∠BOD=∠P+∠D.
(3)根据图(c),试判断∠BPD,∠B,∠D,∠BQD之间的数量关系,并说明理由.
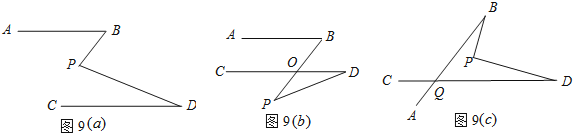
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,对角线AC、BD交于点O,点P在线段BC上(不含点B),∠BPE=![]() ∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
(1)当点P与点C重合时(如图①):
①求证:△BOG≌△POE;②猜想:![]() = ;
= ;
(2)当点P与点C不重合时,如图②,![]() 的值会改变吗?试说明理由.
的值会改变吗?试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线EF分别交平行四边形ABCD边AB、CD于直E、F,将图形沿直线EF对折,点A、D分別落在点A′、D′处.若∠A=60°,AD=4,AB=8,当点A′落在BC边上任意点时,设点P为直线EF上的动点,请直接写出PC+PA′的最小值( )
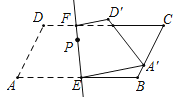
A.4+![]() B.8C.6+
B.8C.6+![]() D.4
D.4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】诗词文化在中国源远流长,其中蕴含着很深的文化内涵,小天参加了学习举办的“诗词大会”,答对最后两道单选题就顺利通关,第一道单选题与第二道单选题均有4个选项,这两道题小天都不会,不过小天还有两个“求助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项).
(1)若小天两次“求助”都在第一道题中使用,则小天答对第一道题的概率是多少?
(2)若小天将每道题各用一次“求助”,请用树状图或列表法,求小天顺利通关的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:
![]() ,
,![]() 分别是什么数时,多项式
分别是什么数时,多项式![]() 和
和![]() 恒等?
恒等?
阅读理解:
所谓恒等式,就是指不论用任何数值来代替式中的变量,左、右两边的值都相等的等式.我们用符号“![]() ”来表示恒等,读作“恒等于”.于是,上面的问题也可以表述为:已知
”来表示恒等,读作“恒等于”.于是,上面的问题也可以表述为:已知![]() ,求待定系数
,求待定系数![]() ,
,![]() .
.
问题解决:
(方法1—数值代入法)由恒等式的概念,我们每用一个数值来代替问题中的![]() ,即可得到一个关于
,即可得到一个关于![]() 与
与![]() 的方程.因此,要求出
的方程.因此,要求出![]() 与
与![]() 的值,只需要用两个不同的数值分别代替式中的
的值,只需要用两个不同的数值分别代替式中的![]() ,就可以得到一个关于
,就可以得到一个关于![]() 与
与![]() 的二元一次方程组,解这个方程组,即可求得
的二元一次方程组,解这个方程组,即可求得![]() 与
与![]() .
.
解:分别用![]() ,
,![]() 代替式中的
代替式中的![]() ,得
,得
![]()
解之,得![]()
(方法2—系数比较法)
定理 如果![]() ,
,
那么![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
根据这个定理,也可以这样解:
解:由题设![]() ,
,
比较对应项的系数,得![]() ,
,![]() .
.
请回答下面的问题:
(1)已知多项式![]() .求
.求![]() 与
与![]() 的值;
的值;
(2)如果![]() 被
被![]() 除后余
除后余![]() ,求
,求![]() 的值及商式.
的值及商式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平行四边形ABCD,延长AD到E,使DE=AD,连接BE与DC交于O点.
(1)求证:△BOC≌△EOD;
(2)当△ABE满足什么条件时,四边形BCED是菱形?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在图中利用网格点和三角板画图或计算:
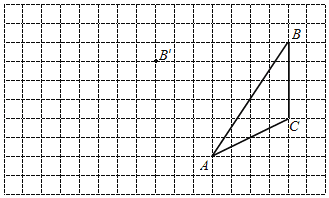
(1)在给定方格纸中画出![]() 平移后的
平移后的![]() (点
(点![]() 的对应点是点
的对应点是点![]() );
);
(2)画出![]() 边上的中线
边上的中线![]() ;
;
(3)画出![]() 边上的高线
边上的高线![]() ;
;
(4)记网格的边长为1,则在平移的过程中线段![]() 扫过区域的面积为
扫过区域的面积为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com