
分析 (1)根据题意可得分式方程:$\frac{1}{1-a}$=$\frac{2}{3}$,解此方程即可求得答案;
(2)首先根据题意求得a2,a3,a4的值,可得规律:an的衍生数3次一循环,继而求得答案.
解答 解:(1)根据题意得:$\frac{1}{1-a}$=$\frac{2}{3}$,
解得a=-$\frac{1}{2}$,
经检验,a=-$\frac{1}{2}$是原分式方程的解.
即a=-$\frac{1}{2}$;
故答案为:$-\frac{1}{2}$;
(2)∵a1=$\frac{1}{3}$,
∴a1的衍生数a2=$\frac{1}{1-(-\frac{1}{3})}$=$\frac{3}{4}$,
a2的衍生数a3=$\frac{1}{1-\frac{3}{4}}$=4,
a3的衍生数a4=$\frac{1}{1-4}$=-$\frac{1}{3}$,
a4的衍生数a5=$\frac{1}{1-(-\frac{1}{3})}$=$\frac{3}{4}$;
∴an的衍生数3次一循环,
∵2015÷3=671…2;
∴a2015=a2=$\frac{3}{4}$,
故答案为:$\frac{3}{4}$.
点评 此题考查了分式方程的求解方法.此题难度适中,属于规律性题目,注意得到规律:an的衍生数3次一循环是解此题的关键.


 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:选择题
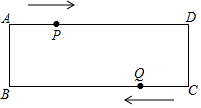 如图,在矩形ABCD中,AB=4cm,AD=12cm,点P在AD边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在这段时间内,线段PQ有( )次平行于AB?
如图,在矩形ABCD中,AB=4cm,AD=12cm,点P在AD边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在这段时间内,线段PQ有( )次平行于AB?| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
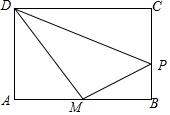 如图,矩形ABCD中,AB=6cm,AD=4cm,点M是边AB的中点,点P是矩形边上的一个动点,点P从M出发在矩形的边上沿着逆时针方向运动,则当点P沿着矩形的边逆时针旋转一周时,△DMP面积刚好为5cm2的时刻有( )
如图,矩形ABCD中,AB=6cm,AD=4cm,点M是边AB的中点,点P是矩形边上的一个动点,点P从M出发在矩形的边上沿着逆时针方向运动,则当点P沿着矩形的边逆时针旋转一周时,△DMP面积刚好为5cm2的时刻有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
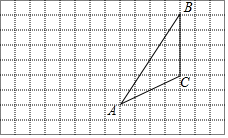 画图并填空:如图,每个小正方形的边长为1个单位,每个小正方形的顶点叫格点.
画图并填空:如图,每个小正方形的边长为1个单位,每个小正方形的顶点叫格点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
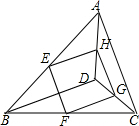 如图,E,F,G,H分别是边AB,BC,CD,DA的中点.
如图,E,F,G,H分别是边AB,BC,CD,DA的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com