
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源:不详 题型:填空题
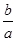 是整数时,满足条件的整数k的值共有 个.
是整数时,满足条件的整数k的值共有 个.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
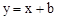 经过点A,C’,则点C’的坐标是 .
经过点A,C’,则点C’的坐标是 .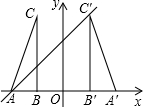
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
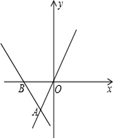
 与x轴、y轴分别交于A、B两点,点M是OB上一点,若直线AB沿AM折叠,点B恰好落在x轴上的点C处,则点M的坐标是
与x轴、y轴分别交于A、B两点,点M是OB上一点,若直线AB沿AM折叠,点B恰好落在x轴上的点C处,则点M的坐标是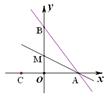
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
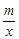 的图像交点坐标为(2,4)、(-4,-2),点(a1,b)(a2,b)分别为一次函数和反比例函数图像上的一点,且a1>a2,则b的取值范围是 .
的图像交点坐标为(2,4)、(-4,-2),点(a1,b)(a2,b)分别为一次函数和反比例函数图像上的一点,且a1>a2,则b的取值范围是 .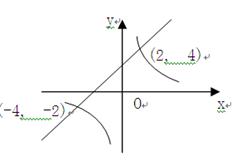
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
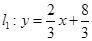 与直线
与直线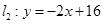 相交于点
相交于点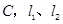 分别交
分别交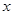 轴
轴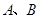 两点.矩形
两点.矩形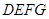 的顶点
的顶点 分别在直线
分别在直线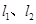 上,顶点
上,顶点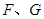 都在
都在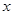 轴上,且点
轴上,且点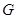 与点
与点 重合.
重合.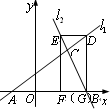
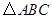 的面积;
的面积;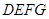 的边
的边 与
与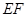 的长;
的长;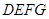 从原点出发,沿
从原点出发,沿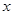 轴的反方向以每秒1个单位长度的速度平移,设移动时间为t(0≤t<3)秒,矩形
轴的反方向以每秒1个单位长度的速度平移,设移动时间为t(0≤t<3)秒,矩形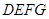 与
与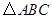 重叠部分的面积为
重叠部分的面积为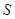 ,求
,求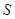 关于的函数关系式.
关于的函数关系式.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| | 到光明社区供水点的路程(千米) | 运费(元/吨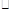 千米) 千米) |
| 甲厂 | 20 | 12 |
| 乙厂 | 14 | 15 |
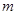 吨,总运费为
吨,总运费为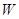 元,试写出
元,试写出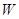 关于
关于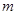 的函数关系式,并求出这天运费最少为多少元?
的函数关系式,并求出这天运费最少为多少元?查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
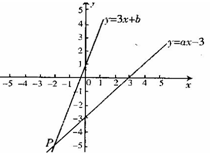
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com