
分析 (1)根据题意求出点A的坐标,利用待定系数法即可解决问题;
(2)分两种情形利用勾股定理计算即可解决问题;
(3)由△APQ≌△ABO可知AP=AB,列出方程求出t,即可解决问题;
解答 (1)解:由AB:y=kx+3可得B(0,3)
又因△ABO的面积=$\frac{9\sqrt{3}}{2}$,
∴$\frac{1}{2}$•AO•BO=$\frac{9\sqrt{3}}{2}$,
∴$\frac{1}{2}$•OA•3=$\frac{9\sqrt{3}}{2}$,
AO=3$\sqrt{3}$,
∵点A在x轴的负半轴,
∴A(-3$\sqrt{3}$,0)
将A(-3$\sqrt{3}$,0)代入y=kx+3解得:k=$\frac{\sqrt{3}}{3}$,
∴直线AB的解析式为:y=$\frac{\sqrt{3}}{3}$x+3.
(2)由题意可列:第一种情况:OP=OA-AP=3$\sqrt{3}$-$\sqrt{3}$t
∵d=PB2=AO2+BO2=(3$\sqrt{3}$-$\sqrt{3}$t)2+32=3t2-18t+36(0<t≤3).
第二种情况:OP=AP-OA=$\sqrt{3}$t-3$\sqrt{3}$
∵d=PB2=AO2+BO2=($\sqrt{3}$t-3$\sqrt{3}$)2+32=3t2-18t+36(t>3).
综上所述:d与t的函数关系式是:d=3t2-18t+36(t>0).
(3)∵∠BAO=∠PAO
∠AOB=∠AQP=90°
∴当AP=AB时△APQ≌△ABO,
∵AB=$\sqrt{A{O}^{2}+B{O}^{2}}$=6,
∴,$\sqrt{3}$t=6,解得:t=2$\sqrt{3}$,
∴此时d=3t2-18t+36=3×(2$\sqrt{3}$)2-18×2$\sqrt{3}$+36=72-36$\sqrt{3}$.
点评 本题考查一次函数综合题,待定系数法,勾股定理等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源:2017届广东省梅州市九年级下学期第一次月考数学试卷(解析版) 题型:解答题
某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求,商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润不低于25%(不考虑其他因素),那么每件衬衫的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
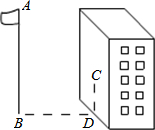 如图,某同学相测量旗杆的高度,他在某一时刻测得1米长的竹竿竖直放置时影长1.5米,在同时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上影长为21米,留在墙上的影高为2米,求旗杆的高度.
如图,某同学相测量旗杆的高度,他在某一时刻测得1米长的竹竿竖直放置时影长1.5米,在同时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上影长为21米,留在墙上的影高为2米,求旗杆的高度.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一次函数y=kx+b(k≠0)的图象经过点(-1,-4)和(2,2)
一次函数y=kx+b(k≠0)的图象经过点(-1,-4)和(2,2)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com