
分析 (1)根据抛物线的对称轴方程进行证明;
(2)根据抛物线与x轴的交点问题可判断抛物线y=ax2+bx-8(a≠0)与x轴的一个交点坐标为(4,0),然后利用抛物线的对称性可得到抛物线y=ax2+bx-8(a≠0)与x轴的另一个交点坐标为(-2,0),从而得到方程ax2+bx-8=0另一个根.
解答 (1)证明:∵抛物线的对称轴是x=1,
∴-$\frac{b}{2a}$=1,
∴2a+b=0;
(2)解:∵关于x的方程ax2+bx-8=0有一个根为4,
∴抛物线y=ax2+bx-8(a≠0)与x轴的一个交点坐标为(4,0),
∵抛物线的对称轴是x=1,
∴抛物线y=ax2+bx-8(a≠0)与x轴的另一个交点坐标为(-2,0),
∴关于x的方程ax2+bx-8=0,有一个根为-2.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标转化为解关于x的一元二次方程;通过二次函数的交点式:y=a(x-x1)(x-x2)(a,b,c是常数,a≠0)可直接得到抛物线与x轴的交点坐标(x1,0),(x2,0).


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
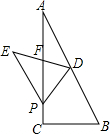 在Rt△ABC中,BC=4,AC=8,点D为AB的中点,P为AC边上一动点.△BDP沿着PD所在的直线翻折,点B的对应点为E.
在Rt△ABC中,BC=4,AC=8,点D为AB的中点,P为AC边上一动点.△BDP沿着PD所在的直线翻折,点B的对应点为E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
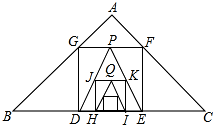 如图,已知Rt△ABC中,AB=AC=3$\sqrt{2}$,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD,PE,值△PDE内作第二个内接正方形HIKJ;再取线段JK的中点Q,在△QHI内作第三个内接正方形;…依次进行下去,则第n个内接正方形的面积为$\frac{1}{{4}^{n-2}}$(n为正整数).
如图,已知Rt△ABC中,AB=AC=3$\sqrt{2}$,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD,PE,值△PDE内作第二个内接正方形HIKJ;再取线段JK的中点Q,在△QHI内作第三个内接正方形;…依次进行下去,则第n个内接正方形的面积为$\frac{1}{{4}^{n-2}}$(n为正整数).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,则∠ADB的度数为( )
如图,AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,则∠ADB的度数为( )| A. | 40° | B. | 60° | C. | 80° | D. | 100° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
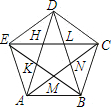 已知:如图,连结正五边形ABCDE各条对角线,就得到一个五角星图案,
已知:如图,连结正五边形ABCDE各条对角线,就得到一个五角星图案,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 该校七年级学生是总体 | B. | 该校七年级的每一个学生是个体 | ||
| C. | 抽出的60名学生是样本 | D. | 样本容量是60 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
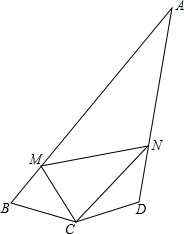 如图,四边形ABCD中,∠B+∠D=180°,∠BCD=150°,CB=CD,M,N为AB、AD上的两个动点,且∠MCN=75°.求证:MN=BM+DN.
如图,四边形ABCD中,∠B+∠D=180°,∠BCD=150°,CB=CD,M,N为AB、AD上的两个动点,且∠MCN=75°.求证:MN=BM+DN.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com