
分析 因为三个方程中c的系数相同,应用加减法来解.
解答 解:$\left\{\begin{array}{l}{a-b+c=2①}\\{4a+2b+c=17②}\\{5a+4b+c=24③}\end{array}\right.$,
②-①得:a+b=5④,
③-①得:4a+5b=22⑤,
把④代入⑤得:20-4b+5b=22,
解得:b=2,
把b=2代入④得:a=3,
把a=3,b=2代入①得:c=1,
所以方程组的解是:$\left\{\begin{array}{l}{a=3}\\{b=2}\\{c=1}\end{array}\right.$.
点评 解三元一次方程组要注意以下几点:
方程组有三个未知数,每个方程的未知项的次数都是1,并且一共有三个方程,像这样的方程组,叫三元一次方程组.通过解方程组,了解把“三元”转化为“二元”、把“二元”转化为“一元”的消元的思想方法,从而进一步理解把“未知”转化为“已知”和把复杂问题转化为简单问题的思想方法.解三元一次方程组的关键是消元.解题之前先观察方程组中的方程的系数特点,认准易消的未知数,消去未知数,组成元该未知数的二元一次方程组.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:解答题
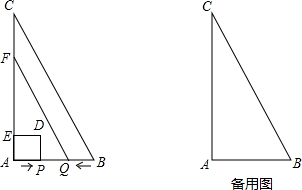
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 等边三角形有三条对称轴 | |
| B. | 线段AB只有一条对称轴 | |
| C. | 等腰三角形的对称轴是底边上的中线 | |
| D. | 等腰三角形的对称轴是底边上的高所在的直线 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
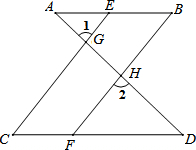 如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 320<x<340 | B. | 320≤x<340 | C. | 320<x≤340 | D. | 320≤x≤340 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
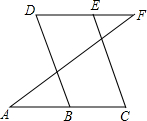 填写理由:如图所示
填写理由:如图所示查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com