
【题目】已知,点![]() 和三角形
和三角形![]() 在同一平面内.
在同一平面内.

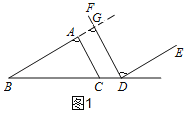
(1)如图1,点![]() 在
在![]() 边上,
边上,![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]() .若
.若![]() ,求
,求![]() 的度数.
的度数.
(2)如图2,点![]() 在
在![]() 的延长线上,
的延长线上,![]() ,
,![]() ,证明:
,证明:![]() .
.
(3)点![]() 是三角形
是三角形![]() 外部的任意一点,过
外部的任意一点,过![]() 作
作![]() 交直线
交直线![]() 于
于![]() ,
,![]() 交直线
交直线![]() 于
于![]() ,直接写出
,直接写出![]() 与
与![]() 的数量关系(不需证明).
的数量关系(不需证明).
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() 或
或![]()
【解析】
根据题意可知:(1)通过![]() 得到两同位角
得到两同位角![]() ,
,![]() 得到两内错角
得到两内错角![]() ,然后等量代换.(2)通过延长BA,构造出新的角
,然后等量代换.(2)通过延长BA,构造出新的角![]() ,再用等量代换找到内错角
,再用等量代换找到内错角![]() ,从而证明直线平行.(3)直线BA与直线AC相交分成四部分,分别考虑这四部分且在三角形
,从而证明直线平行.(3)直线BA与直线AC相交分成四部分,分别考虑这四部分且在三角形![]() 外部的点,可知只有
外部的点,可知只有![]() 或
或![]() 这两种情况.
这两种情况.
(1)∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ;
;
(2)证明:如图1,延长![]() 交
交![]() 于
于![]() .
.
∵![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
∴![]() .
.
(3)![]() 或
或![]()
证明如下:
① 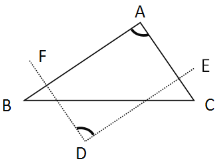
按题意画出图形如上所示:
因为![]() ,
,![]()
所以四边形AEDF是平行四边形(两组对边平行的四边形是平行四边形)
所以![]() (平行四边形对角相等)
(平行四边形对角相等)
② 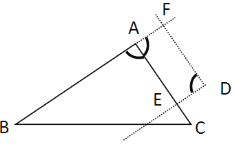
按题意画出图形如上所示:
因为![]() ,
,![]()
所以四边形AEDF是平行四边形(两组对边平行的四边形是平行四边形)
所以![]()
![]() (平行四边形对角相等)
(平行四边形对角相等)
又因为![]()
所以![]()
![]() 即为原图中的
即为原图中的![]()
![]() 即为原图中的
即为原图中的![]() ,即
,即![]()
故答案为![]() 或
或![]()


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
【题目】阅读下面“将无限循环小数化为分数”材料,并解决相应问题:
我们知道分数![]() 写为小数形式即为
写为小数形式即为![]() ,反之,无限循环小数
,反之,无限循环小数![]() 写成分数形式即
写成分数形式即![]() .一般地,任何一个无限循环小数都可以写成分数形式吗?如果可以,应怎样写呢?
.一般地,任何一个无限循环小数都可以写成分数形式吗?如果可以,应怎样写呢?
(发现)先以无限循环小数![]() 为例进行讨论.
为例进行讨论.
设![]() =x,由
=x,由![]() =0.777…可知,10x=7.777…,即10x﹣x=7.解方程,得x=
=0.777…可知,10x=7.777…,即10x﹣x=7.解方程,得x=![]() .于是
.于是![]() =
=![]() ,
,
(类比探究)再以无限循环小数![]() 为例,做进一步的讨论.
为例,做进一步的讨论.
无限循环小数![]() =0.737373…,它的循环节有两位,类比上面的讨论可以想到如下做法.
=0.737373…,它的循环节有两位,类比上面的讨论可以想到如下做法.
设![]() =x,由
=x,由![]() =0.737373…可知,100x=73.7373…,所以100x﹣x=73.解方程,得x=
=0.737373…可知,100x=73.7373…,所以100x﹣x=73.解方程,得x=![]() ,于是得
,于是得![]() =
=![]()
(解决问题)
(1)请你把无限小数![]() 写成分数形式,即
写成分数形式,即![]() = ;
= ;
(2)请你把无限小数![]() 写成分数形式,即
写成分数形式,即![]() = ;
= ;
(3)根据以上过程比较![]() 与1的大小关系,并说明你的理由.
与1的大小关系,并说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器超市销售每台进价分别为160元、120元的A、B两种型号的电风扇,如表是近两周的销售情况:(进价、售价均保持不变,利润=销售收入﹣进货成本)
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 4台 | 1200元 |
第二周 | 5台 | 6台 | 1900元 |
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机小李某天上午营运时是在东西走向的大街上进行的,如果规定向东为正,向西为负,他这天上午所接六位乘客的行车里程(单位:![]() )如下:
)如下:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
问:(1)将最后一位乘客送到目的地时,小李在什么位置?
(2)若汽车耗油量为![]() (升/千米),这天上午小李接送乘客,出租车共耗油多少升?
(升/千米),这天上午小李接送乘客,出租车共耗油多少升?
(3)若出租车起步价为8元,起步里程为![]() (包括
(包括![]() ),超过部分每千米1.2元,问小李这天上午共得车费多少元?
),超过部分每千米1.2元,问小李这天上午共得车费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,点E、F在BD上,且BF=DE.
(1)写出图中所有你认为全等的三角形;
(2)延长AE交BC的延长线于G,延长CF交DA的延长线于H(请补全图形),证明四边形AGCH是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景点试开放期间,团队收费方案如下:不超过30人时,人均收费120元;超过30人且不超过m(30<m≤100)人时,每增加1人,人均收费降低1元;超过m人时,人均收费都按照m人时的标准.设景点接待有x名游客的某团队,收取总费用为y元.
(1)求y关于x的函数表达式;
(2)景点工作人员发现:当接待某团队人数超过一定数量时,会出现随着人数的增加收取的总费用反而减少这一现象.为了让收取的总费用随着团队中人数的增加而增加,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
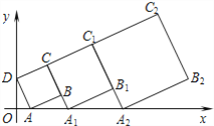
【题目】在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,………按这样的规律进行下去,正方形A2018B2018C2018C2017的面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
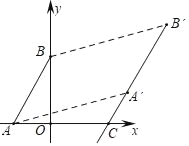
【题目】如图,已知A(﹣2,0),B(0,4),将线段AB平移到第一象限得线段A′B′,点A′的横坐标为5,若作直线A′B′交x轴于点C(4,0).
(1)求线段AB所在直线的解析式;
(2)直线AB上一点P(m,n),求出m、n之间的数量关系;
(3)若点Q在y轴上,求QA′+QB′的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com