
【题目】如图,抛物线y=ax2+bx过A(4,0) B(1,3)两点,点C 、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H
(1)求抛物线的解析式.
(2)直接写出点C的坐标,并求出△ABC的面积.
(3)点P是抛物线BA段上一动点,当△ABP的面积为3时,求出点P的坐标.
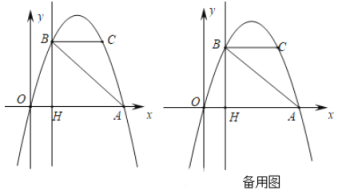
【答案】(1)y=-x2+4x;(2)点C的坐标为(3,3),3;(3)点P的坐标为(2,4)或(3,3)
【解析】
(1)将点A、B的坐标代入即可求出解析式;
(2)求出抛物线的对称轴,根据对称性得到点C的坐标,再利用面积公式即可得到三角形的面积;
(3)先求出直线AB的解析式,过P点作PE∥y轴交AB于点E,设其坐标为P(a,-a2+4a),得到点E的坐标为(a,-a+4),求出线段PE,即可根据面积相加关系求出a,即可得到点P的坐标.
(1)把点A(4,0),B(1,3)代入抛物线y=ax2+bx中,得
![]() ,得
,得![]() ,
,
∴抛物线的解析式为y=-x2+4x;
(2)∵![]() ,
,
∴对称轴是直线x=2,
∵B(1,3),点C 、B关于抛物线的对称轴对称,
∴点C的坐标为(3,3),BC=2,
点A的坐标是(4,0),BH⊥x轴,
∴S△ABC= ![]() =
=![]() ;
;
(3)设直线AB的解析式为y=mx+n,将B,A两点的坐标代入
得![]() ,解得
,解得![]() ,
,
∴y=-x+4,
过P点作PE∥y轴交AB于点E,P点在抛物线y=-x2+4x的AB段,
设其坐标为(a,-a2+4a),其中1<a<4,则点E的坐标为(a,-a+4),
∴PE=(-a2+4a)-( -a+4)=-a2+5a-4,
∴S△ABP= S△PEB+ S△PEA=![]() ×PE×3=
×PE×3=![]() (-a2+5a-4)=
(-a2+5a-4)=![]() ,
,
得a1=2,a2=3,
P1(2,4),P2(3,3)即点C,
综上所述,当△ABP的面积为3时,点P的坐标为(2,4)或(3,3).


科目:初中数学 来源: 题型:
【题目】图1是一个小朋友玩“滚铁环”的游戏,铁环是圆形的,铁环向前滚动时,铁环钩保持与铁环相切.将这个游戏抽象为数学问题,如图2.已知铁环的半径为25 cm,设铁环中心为O,铁环钩与铁环相切点为M,铁环与地面接触点为A,∠MOA=α,且sinα=![]() .
.
(1)求点M离地面AC的高度BM;
(2)设人站立点C与点A的水平距离AC=55 cm,求铁环钩MF的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算能力是数学的基本能力,为了进一步了解学生的计算情况,初2020级数学老师们对某次考试中第19题计算题的得分情况进行了调查,现分别从A、B两班随机各抽取10名学生的成绩如下:
A班10名学生的成绩绘成了条形统计图,如下图,

B班10名学生的成绩(单位:分)分别为:9,8,9,10,9,7,9,8,10,8
经过老师对所抽取学生成绩的整理与分析,得到了如下表数据:
A班 | B班 | |
平均数 | 8.3 | a |
中位数 | b | 9 |
众数 | 8或10 | c |
极差 | 4 | 3 |
方差 | 1.81 | 0.81 |
根据以上信息,解答下列问题.
(1)补全条形统计图;
(2)直接写出表中a,b,c的值:a= ,b= ,c= ;
(3)根据以上数据,你认为A、B两个班哪个班计算题掌握得更好?请说明理由(写出其中两条即可): .
(4)若9分及9分以上为优秀,若A班共55人,则A班计算题优秀的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂家销售一种产品,现准备从网上销售和市场直销两种销售方案中选择一种进行销售.由于受各种不确定因素影响,不同销售的方案会产生不同的成本和其它费用.设每月销售x件,网上销售月利润为w网(元),市场直销月利润为w市(元),具体信息如表:
每件售价(元) | 每件成本(元) | 月其他费用(元) | |
网上销售 | - | 20 | 45000 |
市场直销 | 120 | k |
|
其中k为常数,且30≤k≤50.月利润=月销售额-月成本-月其它费用.
(1)当x=500时,网上销售单价为______元.
(2)分别求出w网,w市与x间的函数解析式(不必写x的取值范围).
(3)若网上销售月利润的最大值与市场直销月利润的最大值相同,求k的值.
(4)如果某月要将3000件产品全部销售完,请你通过分析帮厂家做出决策,选择在网上销售还是市场直销才能使月利润较大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了推动课堂教学改革,打造高效课堂,配合我市“两型课堂”的课题研究,莲城中学对八年级部分学生就一期来“分组合作学习”方式的支持程度进行调查,统计情况如图.试根据图中提供的信息,

回答下列问题:
(1)求本次被调查的八年级学生的人数,并补全条形统计图;
(2)若该校八年级学生共有180人,请你估计该校八年级有多少名学生支持“分组合作学习”方式(含“非常喜欢”和“喜欢”两种情况的学生).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】港珠澳大桥,从2009年开工建造,于2018年10月24日正式通车.其全长55公里,连接港珠澳三地,集桥、岛、隧于一体,是世界上最长的跨海大桥.如图是港珠澳大桥的海豚塔部分效果图,为了测得海豚塔斜拉索顶端A距离海平面的高度,先测出斜拉索底端C到桥塔的距离(CD的长)约为100米,又在C点测得A点的仰角为30°,测得B点的俯角为20°,求斜拉索顶端A点到海平面B点的距离(AB的长).(已知![]() ≈1.73,tan20°≈0.36,结果精确到0.1)
≈1.73,tan20°≈0.36,结果精确到0.1)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,正方形ABCD的顶点分别为A(0,4)、B(﹣4,0)、C(0,﹣4)、D(4,0),对于图形M,给出如下定义:点P为图形M上任意一点,点Q为正方形ABCD边上任意一点,如果P、Q两点间的距离有最大值,那么称这个最大值为图形M的“正方距”,记作d(M).
(1)已知点E(0,2),G(﹣1,﹣1).
①如图1,直接写出d(点E),d(点G)的值;
②如图2,扇形EOF圆心角∠EOF=45°,将扇形EOF绕点O顺时针旋转α角(0<α<180°)得到扇形E'OF',当d(扇形E'OF')取最大值时,求α角的取值范围;
(2)点P为平面内一动点,且满足d(点P)=6,直接写出OP长度的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
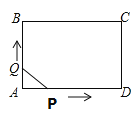
【题目】已知:如图,矩形ABCD中,AB=2cm,AD=3cm.点P和点Q同时从点A出发,点P以3cm/s的速度沿A→D方向运动到点D为止,点Q以2cm/s的速度沿A→B→C→D方向运动到点D为止,则△APQ的面积S(cm2)与运动时间t(s)之间函数关系的大致图象是( )
A.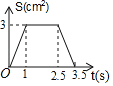 B.
B.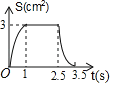
C.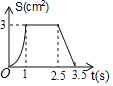 D.
D.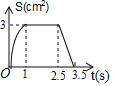
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,AB=AC=5,BC=6,AD是BC边上的中线,四边形ADBE是平行四边形.
(1)求证:四边形ADBE是矩形;
(2)求矩形ADBE的面积.
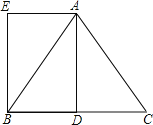
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com