

分析 首先根据题意画出图形,然后由AC是四边形ABCD的和谐线,可以得出△ACD是等腰三角形,从图1,图2,图3三种情况运用等边三角形的性质,正方形的性质和30°的直角三角形性质就可以求出∠BCD的度数.
解答 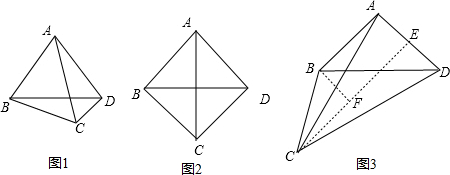 解:∵AC是四边形ABCD的和谐线,
解:∵AC是四边形ABCD的和谐线,
∴△ACD是等腰三角形.
∵AB=AD=BC,
如图1,当AD=AC时,
∴AB=AC=BC,∠ACD=∠ADC
∴△ABC是正三角形,
∴∠BAC=∠BCA=60°.
∵∠BAD=90°,
∴∠CAD=30°,
∴∠ACD=∠ADC=75°,
∴∠BCD=60°+75°=135°.
如图2,当AD=CD时,
∴AB=AD=BC=CD.
∵∠BAD=90°,
∴四边形ABCD是正方形,
∴∠BCD=90°;
如图3,当AC=CD时,过点C作CE⊥AD于E,过点B作BF⊥CE于F,
∵AC=CD.CE⊥AD,
∴AE=$\frac{1}{2}$AD,∠ACE=∠DCE.
∵∠BAD=∠AEF=∠BFE=90°,
∴四边形ABFE是矩形.
∴BF=AE.
∵AB=AD=BC,
∴BF=$\frac{1}{2}$BC,
∴∠BCF=30°.
∵AB=BC,
∴∠ACB=∠BAC.
∵AB∥CE,
∴∠BAC=∠ACE,
∴∠ACB=∠ACE=$\frac{1}{2}$∠BCF=15°,
∴∠BCD=15°×3=45°.
综上:∠BCD的度数是:135°,90°或45°.
点评 此题考查了等腰三角形的性质、矩形的性质、正方形的性质以及含30°角的直角三角形的性质.此题难度较大,注意掌握数形结合思想与分类讨论思想的应用.


科目:初中数学 来源: 题型:填空题
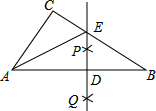 如图,在△ABC中,∠C=90°,∠CAB=62°,按以下步骤作图:
如图,在△ABC中,∠C=90°,∠CAB=62°,按以下步骤作图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x=1,y=3 | B. | x=4,y=1 | C. | x=3,y=2 | D. | x=2,y=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知函数y=$\frac{4}{x}$(x>0)的图象上的三个点A、B、C,他们的横、纵坐标均为正整数,分别过这些点向x轴或y轴作垂线段,以垂线段为边长做正方形,在正方形内以边长为半径作四分之一的圆周的两条弧,组成如图的三个阴影部分,则这三个阴影部分的面积总和是3π-6.
已知函数y=$\frac{4}{x}$(x>0)的图象上的三个点A、B、C,他们的横、纵坐标均为正整数,分别过这些点向x轴或y轴作垂线段,以垂线段为边长做正方形,在正方形内以边长为半径作四分之一的圆周的两条弧,组成如图的三个阴影部分,则这三个阴影部分的面积总和是3π-6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com