
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a>0)与x轴相交于点A(﹣1,0)和点B,与y轴交于点C,对称轴为直线x=1.
(1)求点C的坐标(用含a的代数式表示);
(2)联结AC、BC,若△ABC的面积为6,求此抛物线的表达式;
(3)在第(2)小题的条件下,点Q为x轴正半轴上一点,点G与点C,点F与点A关于点Q成中心对称,当△CGF为直角三角形时,求点Q的坐标.

【答案】(1)C(0,﹣3a);(2) y=x2﹣2x﹣3;(3) Q的坐标为(4,0)或(9,0)
【解析】试题分析:(1)由A点坐标和二次函数的对称性可求出B点的坐标为(3,0),根据两点式写出二次函数解析式,再令y=0,求出y的值,即可的点C的坐标;
(2)由A(﹣1,0),B(3,0),C(0,﹣3a),求出AB、OC的长,然后根据△ABC的面积为6,列方程求出a的值;
(3)设点Q的坐标为(m,0).过点G作GH⊥x轴,垂足为点H,如图,分两种情况求解:当Rt△QGH∽Rt△GFH时,求得m的一个值;当Rt△GFH∽Rt△FCO时,求得m的另一个值.
解:(1)∵抛物线y=ax2+bx+c(a>0)的对称轴为直线x=1,
而抛物线与x轴的一个交点A的坐标为(﹣1,0)
∴抛物线与x轴的另一个交点B的坐标为(3,0)
设抛物线解析式为y=a(x+1)(x﹣3),
即y=ax2﹣2ax﹣3a,
当x=0时,y=﹣3a,
∴C(0,﹣3a);
(2)∵A(﹣1,0),B(3,0),C(0,﹣3a),
∴AB=4,OC=3a,
∴S△ACB=![]() ABOC=6,
ABOC=6,
∴6a=6,解得a=1,
∴抛物线解析式为y=x2﹣2x﹣3;
(3)设点Q的坐标为(m,0).过点G作GH⊥x轴,垂足为点H,如图,
∵点G与点C,点F与点A关于点Q成中心对称,
∴QC=QG,QA=QF=m+1,QO=QH=m,OC=GH=3,
∴OF=2m+1,HF=1,
当∠CGF=90°时,
∵∠QGH+∠FGH=90°,∠QGH+∠GQH=90°,
∴∠GQH=∠HGF,
∴Rt△QGH∽Rt△GFH,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得m=9,
,解得m=9,
∴Q的坐标为(9,0);
当∠CFG=90°时,
∵∠GFH+∠CFO=90°,∠GFH+∠FGH=90°,
∴∠CFO=∠FGH,
∴Rt△GFH∽Rt△FCO,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得m=4,
,解得m=4,
∴Q的坐标为(4,0);
∠GCF=90°不存在,
综上所述,点Q的坐标为(4,0)或(9,0).



科目:初中数学 来源: 题型:
【题目】已知点M(n,﹣n )在第二象限,过点M的直线y=kx+b(0<k<1)分别交x轴、y轴于点A,B,过点M作MN⊥x轴于点N,则下列点在线段AN的是( )
A. ((k﹣1)n,0) B. ((k+![]() )n,0)) C. (
)n,0)) C. (![]() ,0) D. ((k+1)n,0)
,0) D. ((k+1)n,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=9,AB=12,BC=15,P为BC边上一动点,PG⊥AC于点G,PH⊥AB于点H.
(1)求证:四边形AGPH是矩形;
(2)在点P的运动过程中,GH的长度是否存在最小值?若存在,请求出最小值,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角![]() 内部,画1条射线,可得3个锐角;画2条不同射线,可得6个锐角;画3条不同射线,可得10个锐角;…….照此规律,画6条不同射线,可得锐角________个.
内部,画1条射线,可得3个锐角;画2条不同射线,可得6个锐角;画3条不同射线,可得10个锐角;…….照此规律,画6条不同射线,可得锐角________个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明的家在某住宅楼AB的最顶层(AB⊥BC),他家的后面有一建筑物CD(CD∥AB),他很想知道这座建筑物的高度,于是在自家阳台的A处测得建筑物CD的底部C的俯角是43°,顶部D的仰角是25°,他又测得两建筑物之间的距离BC是28米,请你帮助小明求出建筑物CD的高度(精确到1米).
(参考数据:sin25°≈0.42,cos25°≈0.91,tan25°≈0.47;sin43°≈0.68,cos43°≈0.73,tan43°≈0.93.)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上有A,B,C三点,分别代表﹣30,﹣10,10,两只电子蚂蚁甲,乙分别从A,C两点同时相向而行,甲的速度为4个单位/秒,乙的速度为6个单位/秒.
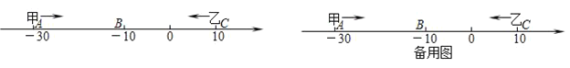
(1)甲,乙经过多少秒在数轴上相遇,并求出相遇点表示的数?
(2)多少秒后,甲到A,B,C的距离和为48个单位?
(3)在甲到A、B、C的距离和为48个单位时,若甲调头并保持速度不变,则甲,乙还能在数轴上相遇吗?若能,求出相遇点;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G.F为AB边上一点,连接CF,且∠ACF=∠CBG.
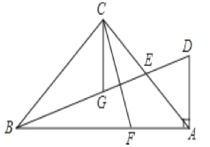
(1)求证:BG=CF;
(2)求证:CF=2DE;
(3)若DE=1,求AD的长
查看答案和解析>>
科目:初中数学 来源: 题型:
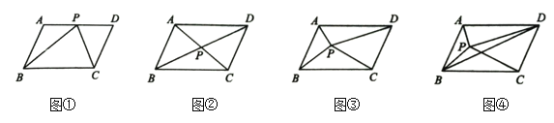
【题目】如图,四边形![]() 是面积为
是面积为![]() 的平行四边形,其中
的平行四边形,其中![]() .
.
(1)如图①,点![]() 为
为![]() 边上任意一点,则
边上任意一点,则![]() 的面积
的面积![]() 和
和![]() 的面积
的面积![]() 之和与
之和与![]() 的面积
的面积![]() 之间的数量关系是__________;
之间的数量关系是__________;
(2)如图②,设![]() 交于点
交于点![]() ,则
,则![]() 的面积
的面积![]() 和
和![]() 的面积
的面积![]() 之和与
之和与![]() 的面积
的面积![]() 之间的数量关系是___________;
之间的数量关系是___________;
(3)如图③,点![]() 为
为![]() 内任意一点时,试猜想
内任意一点时,试猜想![]() 的面积
的面积![]() 和
和![]() 的面积
的面积![]() 之和与
之和与![]() 的面积
的面积![]() 之间的数量关系,并加以证明;
之间的数量关系,并加以证明;
(4)如图④,已知点![]() 为
为![]() 内任意一点,
内任意一点,![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,连接
,连接![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
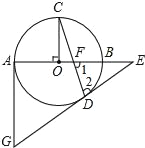
【题目】如图的⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,并与AB延长线交于点E.
(1)求证:∠1=∠2.
(2)已知:OF:OB=1:3,⊙O的半径为3,求AG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com