
【题目】用尺规在一个平行四边形内作菱形ABCD,下列作法中错误的是( )
A. 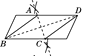 B.
B. 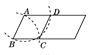 C.
C. 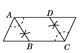 D.
D. 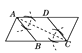
【答案】C
【解析】
首先要理解每个图的作法,作的辅助线所具有的性质,再根据平行四边形的性质和菱形的判定定理判定.
A、作的辅助线AC是BD的垂直平分线,由平行四边形中心对称图形的性质可得AC与BD互相平分且垂直,则四边形ABCD是菱形,故A不符合题意;
B、由辅助线可得AD=AB=BC,由平行四边形的性质可得AD//BC,则四边形ABCD是菱形,故B不符合题意;
C、辅助线AB、CD分别是原平行四边形一组对角的角平分线,只能说明四边形ABCD是平行四边形,故C符合题意;
D、此题的作法是:连接AC,分别作两个角与已知角∠CAD、∠ACB相等的角,即∠BAC=∠DAC,∠ACB=∠ACD,
由AD//BC,得∠BAD+∠ABC=180°,
∠BAC=∠DAC=∠ACB=∠ACD,
则AB=BC,AD =CD,∠BAD=∠BCD,
则∠BCD+∠ABC=180°,
则AB//CD,
则四边形ABCD是菱形,
故D不符合题意.
故答案为C.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】△ABC和△ECD都是等边三角形

(1)如图1,若B、C、D三点在一条直线上,求证:BE=AD;
(2)保持△ABC不动,将△ECD绕点C顺时针旋转,使∠ACE=90°(如图2),BC与DE有怎样的位置关系?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC中,∠ACB=90°,AC=6cm,BC =8cm.点P从A点出发,沿![]() 路径向终点B运动,点Q从B点出发,沿
路径向终点B运动,点Q从B点出发,沿![]() 路径向终点A运动.点P 和Q分别
路径向终点A运动.点P 和Q分别![]() 和
和![]() 的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过点P和Q作PE⊥l于E,QF⊥l于F.则点P运动多少秒时,△PEC和△CFQ全等?请说明理由.
的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过点P和Q作PE⊥l于E,QF⊥l于F.则点P运动多少秒时,△PEC和△CFQ全等?请说明理由.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“今天你光盘了吗?”这是国家倡导“厉行节约,反对浪费”以来的时尚流行语.某校团委随机抽取了部分学生,对他们进行了关于“光盘行动”所持态度的调查,并根据调查收集的数据绘制了如下两幅不完整的统计图: 
根据上述信息,解答下列问题:
(1)抽取的学生人数为;
(2)将两幅统计图补充完整;
(3)请你估计该校1200名学生中对“光盘行动”持赞成态度的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题原型:如图①,在等腰直角三角形ABC中,∠ACB=90°,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.过点D作△BCD的BC边上的高DE,
易证△ABC≌△BDE,从而得到△BCD的面积为 ![]() .
.
初步探究:如图②,在Rt△ABC中,∠ACB=90°,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.用含a的代数式表示△BCD的面积,并说明理由.
简单应用:如图③,在等腰三角形ABC中,AB=AC,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.直接写出△BCD的面积.(用含a的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴是x=1,有以下四个结论:
①abc>0;②b2﹣4ac>0;③b=﹣2a;④a+b+c>2,
其中正确的是(填写序号)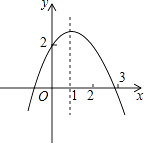
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题与探索
问题情境:课堂上,老师让同学们以“菱形纸片的剪拼”为主题开展数学活动.如图(1),将一张菱形纸片ABCD(∠BAD>90°)沿对角线AC剪开,得到△ABC和△ACD.
操作发现:
(1)将图(1)中的△ACD以点A为旋转中心,按逆时针方向旋转角α,使α=∠BAC,得到如图(2)所示的△AC′D,分别延长BC和DC′交于点E,则四边形ACEC′的形状是 . 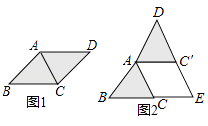
(2)创新小组将图(1)中的△ACD以点A为旋转中心,按逆时针方向旋转角α,使α=2∠BAC,得到如图(3)所示的△AC′D,连接DB、C′C,得到四边形BCC′D,发现它是矩形,请证明这个结论.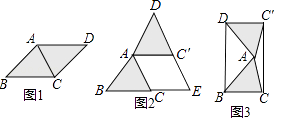
查看答案和解析>>
科目:初中数学 来源: 题型:
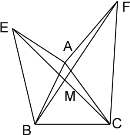
【题目】如图甲所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC. BF与CE相交于点M
(1)求证:①△ACE≌△AFB;②EC⊥BF.
(2)如图乙连接EF,画出△ABC边BC上的高线AD,延长DA交EF于点N,其他条件不变,下列四个结论:①∠EAN=∠ABC;
②△AEN≌△BAD;③![]() ;④EN=FN。
;④EN=FN。
正确的结论是____________(把正确结论的序号全部填上)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com