
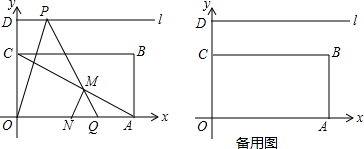
分析 (1)①由四边形OABC是矩形,根据矩形的性质,即可求得点B的坐标;②由正切函数,即可求得∠CAO的度数,③由三角函数的性质,即可求得点P的坐标;
(2)分别从MN=AN,AM=AN与AM=MN去分析求解即可求得答案.
解答 解:(1)①∵四边形OABC是矩形,
∴AB=OC,OA=BC,
∵A(6,0)、C(0,2$\sqrt{3}$),
∴点B的坐标为:(6,2$\sqrt{3}$);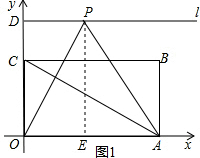
②∵tan∠CAO=$\frac{OC}{OA}$=$\frac{2\sqrt{3}}{6}$=$\frac{\sqrt{3}}{3}$,
∴∠CAO=30°;
③如图1:当点Q与点A重合时,过点P作PE⊥OA于E,
∵∠PQO=60°,D(0,3$\sqrt{3}$),
∴PE=3$\sqrt{3}$,
∴AE=$\frac{PE}{tan60°}$=3,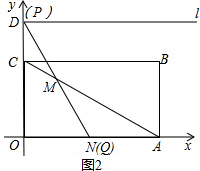
∴OE=OA-AE=6-3=3,
∴点P的坐标为(3,3$\sqrt{3}$);
故答案为:①(6,2$\sqrt{3}$),②30,③(3,3$\sqrt{3}$);
(2)情况①:如图2,MN=AN=3,
则∠AMN=∠MAN=30°,
∴∠MNO=60°,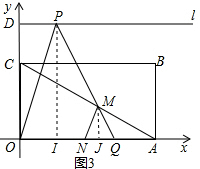
∵∠PQO=60°,
即∠MQO=60°,
∴点N与Q重合,
∴点P与D重合,
∴此时m=0,
情况②,如图3,AM=AN,作MJ⊥x轴、PI⊥x轴;
MJ=MQ•sin60°=AQ•sin60°=(OA-IQ-OI)•sin60°=$\frac{\sqrt{3}}{2}$(3-m)=$\frac{1}{2}$AM=$\frac{1}{2}$AN=$\frac{3}{2}$,
可得$\frac{\sqrt{3}}{2}$(3-m)=$\frac{3}{2}$,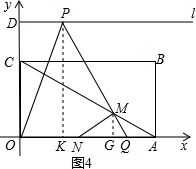
解得:m=3-$\sqrt{3}$,
情况③AM=NM,此时M的横坐标是4.5,
如图4,过点P作PK⊥OA于K,过点M作MG⊥OA于G,
∴MG=$\frac{\sqrt{3}}{2}$,
∴QK=$\frac{PK}{tan60°}$=$\frac{3\sqrt{3}}{\sqrt{3}}$=3,GQ=$\frac{MG}{tan60°}$=$\frac{1}{2}$,
∴KG=3-0.5=2.5,AG=$\frac{1}{2}$AN=1.5,
∴OK=2,
∴m=2.
点评 此题考查了矩形的性质,相似三角形的判定与性质、等腰三角形的性质以及直角三角形的性质等知识.此题综合性较强,难度较大,注意数形结合思想与分类讨论思想的应用.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有一个边长为x的正方体,则它的表面积S与边长x之间的函数关系 | |
| B. | 某梯形的下底5cm,高3cm,上底xcm(0<x<5),则梯形的面积S与上底x之间的函数关系 | |
| C. | 一个质量为100kg的物体,静止放在桌面上,则该物体对桌面的压强P与受力面面积S之间的函数关系 | |
| D. | 一个小球由静止开始沿一个斜坡向下滚动,其速度每秒增加2m/s,则小球速度v与时间t之间的函数关系 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
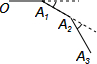 如图,小敏从点0出发,前进10 m到达点A1后,向右转30°前进10m到达点A2,再向
如图,小敏从点0出发,前进10 m到达点A1后,向右转30°前进10m到达点A2,再向查看答案和解析>>
科目:初中数学 来源: 题型:解答题
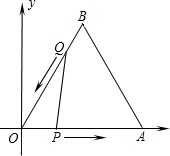 如图,等边△ABO放置在平面直角坐标系中,OA=4,动点P、Q同时从O、B两点出发,分别沿OA、BO方向匀速运动,它们的速度均为每秒1个单位长度,当点P到达点A时,P、Q两点停止运动,设点P的运动时间为x(s)(0<x<4),解答下列问题:
如图,等边△ABO放置在平面直角坐标系中,OA=4,动点P、Q同时从O、B两点出发,分别沿OA、BO方向匀速运动,它们的速度均为每秒1个单位长度,当点P到达点A时,P、Q两点停止运动,设点P的运动时间为x(s)(0<x<4),解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com