
分析 (1)根据左加右减,可得答案;
(2)根据上加下减,可得答案.
解答 解:(1)设平移后积的解析式为y=$\frac{1}{3}$(x+b)2,
由图象过点(1,3),得
$\frac{1}{3}$(1+b)2=3,
解得b=2,b=-4,
y=$\frac{1}{3}$(x+2)2,y=$\frac{1}{3}$(x-4)2;
(2)设平移后的解析式为y=$\frac{1}{3}$x2+b,
直线y=$\frac{1}{2}$x+2与x轴的交点(-4,0).
图象过直线y=$\frac{1}{2}$x+2与x轴的交点,得
$\frac{1}{3}$×(-4)2+b=0,
解得b=-$\frac{16}{3}$.
平移后的解析式为y=$\frac{1}{3}$x2-$\frac{16}{3}$.
点评 本题考查了二次函数图形与几何变换,要求熟练掌握平移的规律:左加右减,上加下减.并用规律求函数解析式.会利用方程求抛物线与坐标轴的交点.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是二次函数y=ax2+bx+c的图象,下列结论:
如图是二次函数y=ax2+bx+c的图象,下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
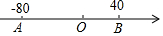 如图,在一条东西方向的马路上O为路边的车站台,A,B两人分别在距离站台东西两侧的80米和40米处,设向东为正,A,B两人各自以一定的速度在马路上行走.且A的行走速度为2米/秒.
如图,在一条东西方向的马路上O为路边的车站台,A,B两人分别在距离站台东西两侧的80米和40米处,设向东为正,A,B两人各自以一定的速度在马路上行走.且A的行走速度为2米/秒.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 李老师用直尺和圆规作已知角的平分线.
李老师用直尺和圆规作已知角的平分线.| A. | SSS | B. | SAS | C. | ASA | D. | AAS |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com