
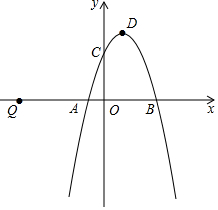
 如图,二次函数y=mx2+(m2-m)x-2m+1的图象与x轴交于点A、B,与y轴交于点C,顶点D的横坐标为1.
如图,二次函数y=mx2+(m2-m)x-2m+1的图象与x轴交于点A、B,与y轴交于点C,顶点D的横坐标为1.分析 (1)利用抛物线的顶点坐标的横坐标为1建立方程即可求出M,进而得出抛物线解析式,再令y=0解一元二次方程即可得出点A,B的坐标;
(2)先构造出全等三角形△EPH≌△PQO,进而得出EH=OP=-t,HP=OQ=5,即可得出点E的坐标,代入抛物线解析式中即可求出t;
(3)分两种情况讨论计算,①点M在x轴上方时,构造相似三角形△MCN∽△DAF得出比例式建立方程即可求出点M的坐标,
②点M在x轴下方时,同①的方法即可得出点M的坐标.
解答 解:(1)∵抛物线的顶点坐标的横坐标为1,
∴$-\frac{{{m^2}-m}}{2m}=1$,
解得,m1=-1,m2=0(舍去)
∴二次函数的表达式为y=-x2+2x+3,
当y=0时,-x2+2x+3=0,
解得,x1=-1,x2=3,
∴A(-1,0),B(3,0),
(2)如图1, 过点E作EH⊥y轴于点H,
过点E作EH⊥y轴于点H,
∵∠PQO+∠OPQ=90°,∠OPQ+∠HPE=90°,
∴∠HPE=∠PQO,
由旋转知,PQ=PE,
在△EPH和△PQO中,$\left\{\begin{array}{l}{∠PHE=∠QOP=90°}\\{∠HPE=∠PQO}\\{PQ=PE}\end{array}\right.$,
∴△EPH≌△PQO,
∴EH=OP=-t,HP=OQ=5
∴E(-t,5+t)
当点E恰好在该二次函数的图象上时,有5+t=-t2-2t+3
解得t1=-2,t2=-1(由于t<-1所以舍去),
(3)设点M(a,-a2+2a+3)
①若点M在x轴上方,
如图2,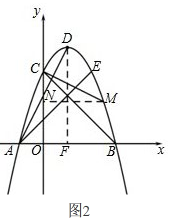 过点M作MN⊥y轴于点N,
过点M作MN⊥y轴于点N,
过点D作DF⊥x轴于点F.
∵∠EAB=∠OCB=45°,∠DAE=∠MCB
∴∠MCN=∠DAF
∴△MCN∽△DAF,
∴$\frac{MN}{DF}=\frac{NC}{FA}$,即$\frac{a}{4}=\frac{{{a^2}-2a}}{2}$
∴${a_1}=\frac{5}{2}$,a2=0(舍去)
∴$M(\frac{5}{2},\frac{7}{4})$,
②若点M在x轴下方,
如图3, 过点M作MN⊥y轴于点N,
过点M作MN⊥y轴于点N,
过点D作DF⊥x轴于点F.
∵∠EAB=∠OCB=45°,∠DAE=∠MCB
∴∠MCN=∠ADF
∴△MCN∽△ADF
∴$\frac{MN}{AF}=\frac{NC}{DF}$,即$\frac{a}{2}=\frac{{{a^2}-2a}}{4}$
∴a1=4,a2=0(舍去)
∴M(4,-5)
综上所述,$M(\frac{5}{2},\frac{7}{4})$或M(4,-5).
点评 此题是二次函数综合题,主要考查了抛物线的顶点坐标,全等三角形的判定和性质,相似三角形的判定和性质,解(2)的关键是构造出△EPH≌△PQO,解(3)的关键是构造出△MCN∽△ADF,是一道中等难度的中考常考题.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题
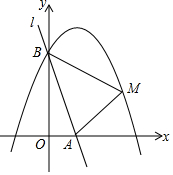 如图,直线l:y=-3x+3与x轴、y轴分别相交于A、B两点,抛物线y=ax2-2ax+a+4(a<0)经过点B.
如图,直线l:y=-3x+3与x轴、y轴分别相交于A、B两点,抛物线y=ax2-2ax+a+4(a<0)经过点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com