
 (千克)随销售单价
(千克)随销售单价 (元/千克)的变化而变化,具体关系式为:
(元/千克)的变化而变化,具体关系式为: ,且物价部门规定这种绿茶的销售单价不得高于90元/千克.设这种绿茶在这段时间内的销售利润为
,且物价部门规定这种绿茶的销售单价不得高于90元/千克.设这种绿茶在这段时间内的销售利润为 (元),解答下列问题:
(元),解答下列问题: 与
与 的关系式;
的关系式; 取何值时,
取何值时, 的值最大?
的值最大?

 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源:不详 题型:解答题
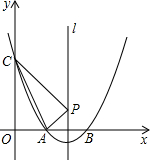
 的图像经过点
的图像经过点 和点B,其中点B在第一象限,且OA=OB,cot∠BAO=2.
和点B,其中点B在第一象限,且OA=OB,cot∠BAO=2.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
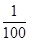 x+150,成本为20元/件,月利润为W内(元);②若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳
x+150,成本为20元/件,月利润为W内(元);②若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳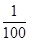 x2元的附加费,月利润为W外(元).
x2元的附加费,月利润为W外(元).查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 轴于点
轴于点 ,交
,交 轴于
轴于 ,
, 两点(点
两点(点 在点
在点 的左侧),已知
的左侧),已知 点坐标为(6,0).
点坐标为(6,0).
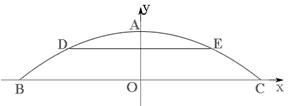
 作线段
作线段 的垂线交抛物线于点
的垂线交抛物线于点 ,如果以点
,如果以点 为圆心的圆与抛物线的对称轴
为圆心的圆与抛物线的对称轴 相切,先补全图形,再判断直线
相切,先补全图形,再判断直线 与⊙
与⊙ 的位置关系并加以证明;
的位置关系并加以证明; 是抛物线上的一个动点,且位于
是抛物线上的一个动点,且位于 ,
, 两点之间.问:当点
两点之间.问:当点 运动到什么位置时,
运动到什么位置时, 的面积最大?求出
的面积最大?求出 的最大面积.
的最大面积.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com