
 x(a-x)=-
x(a-x)=-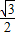 x2+
x2+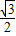 ax=-
ax=-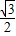 (x-
(x-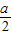 )2+
)2+ a2
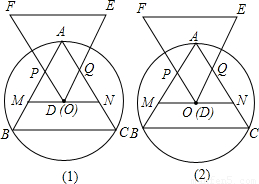
a2 时,即D点位于MN的中点位置时,四边形APDQ的面积最大,且最大值为
时,即D点位于MN的中点位置时,四边形APDQ的面积最大,且最大值为 a2.
a2. a2,而由(2)知S四边形APDQ=
a2,而由(2)知S四边形APDQ= a2
a2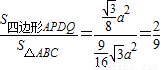 ,
, S△ABC.
S△ABC.

科目:初中数学 来源: 题型:
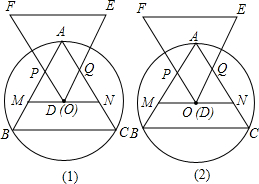 明理由;你能发现四边形APDQ的面积与△ABC的面积有何关系吗?为什么?
明理由;你能发现四边形APDQ的面积与△ABC的面积有何关系吗?为什么?查看答案和解析>>
科目:初中数学 来源:第34章《二次函数》中考题集(51):34.4 二次函数的应用(解析版) 题型:解答题
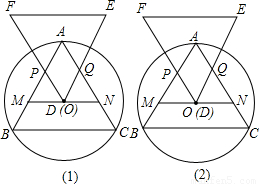
查看答案和解析>>
科目:初中数学 来源:第20章《二次函数和反比例函数》中考题集(47):20.5 二次函数的一些应用(解析版) 题型:解答题
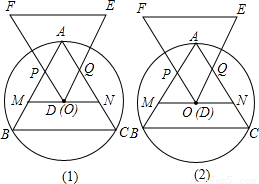
查看答案和解析>>
科目:初中数学 来源:第2章《二次函数》中考题集(47):2.4 二次函数的应用(解析版) 题型:解答题
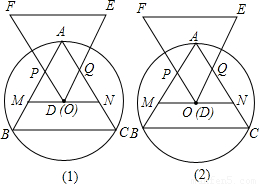
查看答案和解析>>
科目:初中数学 来源:2005年山东省济南市中考数学试卷(课标卷)(解析版) 题型:解答题
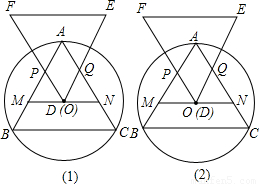
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com