
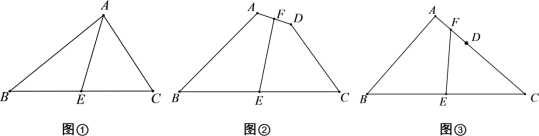
【题目】(发现问题)爱好数学的小强在做作业时碰到这样的一道题目:如图①,在△ABC中,AB=8,AC=6,E为BC中点,求AE的取值范围.
(解决问题)
(1)小强经过多次的尝试与探索,终于得到解题思路:在图①中,作AB边上的中点F,连接EF,构造出△ABC的中位线EF,请你完成余下的求解过程.
(灵活运用)
(2)如图②,在四边形ABCD中,AB=8,CD=6,E、F分别为BC、AD中点,求EF的取值范围.
(3)变式:把图②中的A、D、C变成在一直线上时,如图③,其它条件不变,则EF的取值范围为 .
(迁移拓展)
(4)如图④,在△ABC中,∠A=60°,AB=4,E为BC边的中点,F是AC边上一点且EF正好平分△ABC的周长,则EF= .

【答案】(1)详见解析;(2)1<EF<7;(3)![]() ;(4)EF=
;(4)EF=![]() .
.
【解析】
(1)依照题意作出图形,利用△AFE中两边之和大于第三边,两边之差小于第三边,求解AE边的取值范围;
(2)连接BD,取BD 中点G,连接FG、EG,由E、F分别为BC、AD中点,可得FG=![]() AB,EG=
AB,EG=![]() DC,同(1)△GEF中两边之和大于第三边,两边之差小于第三边,求解EF边的取值范围;
DC,同(1)△GEF中两边之和大于第三边,两边之差小于第三边,求解EF边的取值范围;
(3)如图,连接BD,取BD的中点H,连接HF,HE,由三角形中位线定理可知![]() ,
,![]() ,在△DHE中有,两边之和大于第三边,两边之差小于第三边,即可求得
,在△DHE中有,两边之和大于第三边,两边之差小于第三边,即可求得![]() ;
;
(4)在线段CF上取一点M,使得FM=AF,连接BM,取BM的中点N,连接FN,EN,由EF平分三角形ABC周长,可得CM=AB=4,由三角形中位线定理,及∠A=60°,可知NF=NE=2,且∠FNE=120°,作NO⊥EF于O,解△ENF,可得FO=E0=![]() ,即可求得EF=
,即可求得EF=![]() .
.
(1)解:
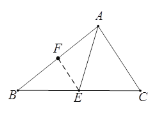
∵E 为 BC 中点,F为 AB 中点,
∴EF=![]() AC,
AC,
∵AB=8,AC=6,
∴AF=![]() AB=4,EF=
AB=4,EF=![]() AC=3,
AC=3,
在△AEF中,两边之和大于第三边,两边之差小于第三边,
∴4-3<AE<4+3,
即,1<AE<7;
(2)解:连接BD,取BD 中点G,连接FG、EG,

∵E、F分别为BC、AD中点,
∴FG=![]() AB,EG=
AB,EG=![]() DC,
DC,
∵AB=8,CD=6,
∴FG=4,EG=3,
在△GEF中,4-3<EF<4+3,
即1<EF<7.
(3)如图,连接BD,取BD的中点H,连接HF,HE,

∵E、F分别为BC、AD中点,
∴![]() ,
,![]()
∴在△DHE中,![]() ,
,
即EF的取值范围为![]() ,
,
故答案为:![]() ;
;
(4)在线段CF上取一点M,使得FM=AF,连接BM,取BM的中点N,连接FN,EN,
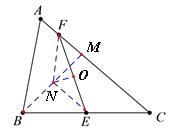
∴F为线段AM的中点,
∵E为BC中点,
∴FN∥AB,且![]() ,EN∥AC,且
,EN∥AC,且![]() ,BE=EC,
,BE=EC,
∵∠A=60°,AB=4,
∴FN=2,∠FNE=120°,
∵EF正好平分△ABC的周长,
∴![]() ,
,
∴![]() ,
,
∴CM=4,
∴NE=2,
∴△FNE为等腰三角形,且∠NFE=∠NEF=30°,
过点N作NO⊥EF于点O,
则FO=OE=![]() ,
,
∴![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
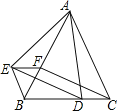
【题目】如图,△ABC和△BEF都是等边三角形,点D在BC边上,点F在AB边上,且∠EAD=60°,连接ED、CF.
(1)求证:△ABE≌△ACD;
(2)求证:四边形EFCD是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好改善河流的水质,治污公司决定购买10台污水处理设备.现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
A型 | B型 | |
价格(万元/台) | a | b |
处理污水量(吨/月) | 240 | 180 |
(1)求a,b的值;
(2)治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() ,试判断
,试判断![]() 与
与![]() 的大小关系,并证明你的结论。
的大小关系,并证明你的结论。
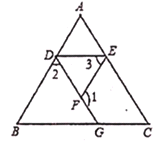
猜想:∠AED=∠C,
理由:∵∠2+∠ADF=180°( ),
∠1+∠2=180°( ),
∴∠1=∠ADF( ),
∴AD∥EF( ),
∴∠3=∠ADE( ),
∵∠3=∠B( ),
∴∠B=∠ADE( ),
∴DE∥BC( ),
∴∠AED=∠C( ),
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】只用无刻度的直尺作图(保留作图痕迹,不要求写作法)
(1)如图1,已知∠AOB,OA=OB,点E在OB边上,其中四边形AEBF是平行四边形,请你在图中画出∠AOB的平分线.
(2)如图2,已知E是菱形ABCD中AB边上的中点,请你在图中画出一个矩形EFGH,使得其面积等于菱形ABCD的一半.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,半径均为1个单位长度的半圆O1,O2,O3,… 组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒![]() 个单位长度,则第2019秒时,点P的坐标是________________
个单位长度,则第2019秒时,点P的坐标是________________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,
b满足 |a+2|+![]() =0,点C的坐标为(0,3).
=0,点C的坐标为(0,3).
(1)求a,b的值及S三角形ABC;
(2)若点M在x轴上,且S三角形ACM=![]() S三角形ABC,试求点M的坐标.
S三角形ABC,试求点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
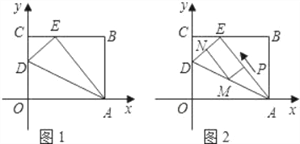
【题目】如图1,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=5,OC=4.
(1)在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D,E两点的坐标;
(2)如图2,若AE上有一动点P(不与A,E重合)自A点沿AE方向E点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为t秒(0<t<5),过P点作ED的平行线交AD于点M,过点M作AE平行线交DE于点N.求四边形PMNE的面积S与时间t之间的函数关系式;当t取何值时,s有最大值,最大值是多少?
(3)在(2)的条件下,当t为何值时,以A,M,E为顶点的三角形为等腰三角形,并求出相应的时刻点M的坐标?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点C在∠AOB的一边OA上,过点C的直线DE∥OB,CF平分∠ACD,CG⊥CF于点C.
(1)若∠O=40°,求∠ECF的度数;
(2)求证:CG平分∠OCD.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com