
如图(1),抛物线 与x轴交于A、B两点,与y轴交于点C(0,
与x轴交于A、B两点,与y轴交于点C(0,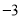 ).[图(2)为解答备用图]
).[图(2)为解答备用图]

(1) __________,点A的坐标为___________,点B的坐标为__________;
__________,点A的坐标为___________,点B的坐标为__________;
(2)设抛物线 的顶点为M,求四边形ABMC的面积;
的顶点为M,求四边形ABMC的面积;
(3)在x轴下方的抛物线上是否存在一点D,使四边形ABDC的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由.
(1) k=-3,A(-1,0),B(3,0);(2)9;(3) 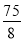 .
.
【解析】
试题分析:(1)将C点坐标代入抛物线的解析式中,即可求出k的值;令抛物线的解析式中y=0,即可求出A、B的坐标;
(2)将抛物线的解析式化为顶点式,即可求出M点的坐标;由于四边形ACMB不规则,可连接OM,将四边形ACMB的面积转化为△ACO、△MOC以及△MOB的面积和;
(3)当D点位于第三象限时四边形ABCD的最大面积显然要小于当D位于第四象限时四边形ABDC的最大面积,因此本题直接考虑点D为与第四象限时的情况即可;设出点D的横坐标,根据抛物线的解析式即可得到其纵坐标;可参照(2)题的方法求解,连接OD,分别表示出△ACO、△DOC以及△DOB的面积,它们的面积和即为四边形ABDC的面积,由此可得到关于四边形ABDC的面积与D点横坐标的函数关系式,根据函数的性质即可求出四边形ABDC的最大面积及对应的D点坐标.
试题解析:(1)由于点C在抛物线的图象上,则有:k=-3;
∴y=x2-2x-3;
令y=0,则x2-2x-3=0,
解得x=-1,x=3,
∴A(-1,0),B(3,0);
(2)抛物线的顶点为M(1,-4),连接OM;
则△AOC的面积=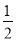 AO•OC=
AO•OC=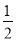 ×1×3=
×1×3=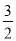 ,
,
△MOC的面积=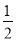 OC•|xM|=
OC•|xM|=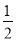 ×3×1=
×3×1=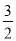 ,
,
△MOB的面积=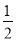 OB•|yM|=
OB•|yM|=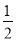 ×3×4=6;
×3×4=6;
∴四边形ABMC的面积=△AOC的面积+△MOC的面积+△MOB的面积=9;
(3)设D(m,m2-2m-3),连接OD;
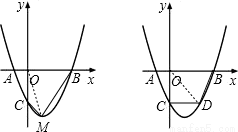
则0<m<3,m2-2m-3<0;
且△AOC的面积=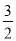 ,△DOC的面积=
,△DOC的面积=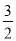 m,△DOB的面积=-
m,△DOB的面积=-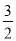 (m2-2m-3);
(m2-2m-3);
∴四边形ABDC的面积=△AOC的面积+△DOC的面积+△DOB的面积
=-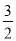 m2+
m2+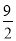 m+6=-
m+6=-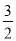 (m-
(m-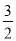 )2+
)2+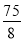 ;
;
∴存在点D(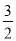 ,-
,-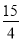 ),使四边形ABDC的面积最大,且最大值为
),使四边形ABDC的面积最大,且最大值为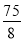 .
.
考点:二次函数综合题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2014-2015学年北京市西城区九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,在正方形ABCD中,有一个小正方形EFGH,其中顶点E,F,G分别在AB,BC,FD上.

(1)求证:△EBF∽△FCD;
(2)连接DH,如果BC=12,BF=3,求tan∠HDG的值.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省心学校九年级上学期数学试卷(解析版) 题型:选择题
已知(5,-1)是双曲线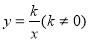 上的一点,则下列各点中不在该图象上的是( )
上的一点,则下列各点中不在该图象上的是( )
A.(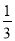 ,-15) B.(5,1) C.(-1,5) D.(10,
,-15) B.(5,1) C.(-1,5) D.(10, )
)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省七年级上学期期中检测数学试卷(解析版) 题型:选择题
若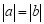 ,则a与b的关系是( )
,则a与b的关系是( )
A.a=b B.a=b C.a=b=0 D.a=b或a=-b
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川中江县继光实验学校九年级上期末模拟考试数学试卷(解析版) 题型:解答题
(1)解方程:
(2)如图,△ABC各顶点的坐标分别为A(4、4),B(-2,2),C(3,0),
①画出它的以原点O为对称中心的△AˊBˊCˊ
②写出 Aˊ,Bˊ,Cˊ三点的坐标。

(3)已知关于x的方程mx2-(m+2)x+2=0(m≠0).
①求证:方程总有两个实数根;
②若方程的两个实数根都是整数,求正整数m的值.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川中江县继光实验学校九年级上期末模拟考试数学试卷(解析版) 题型:选择题
如图,正方形ABCD的边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为s,AE为x,则s关于x的函数图象大致是 ( )
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省自贡市九年级上学期期末统一考试数学试卷(解析版) 题型:解答题
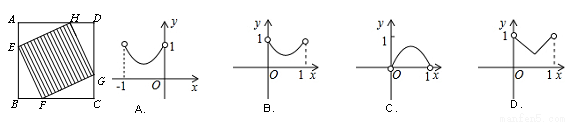
如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,且∠D=2∠CAD.
(1)求∠D的度数;
(2)若CD=1,求BD的长.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省凉山州九年级上学期期末数学试卷(解析版) 题型:选择题
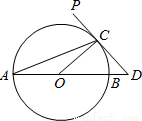
下列图形中,既是轴对称图形又是中心对称图形的有( )个.
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com