练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    作业宝几何计算．
    如图，∠AOD=∠BOC=90°，∠COD=30°，直线EF平分∠COD．
    （1）求∠AOB的度数；
    （2）求∠AOF的度数，你发现了什么？

    解：（1）∵∠AOD=∠BOC=90°，∠COD=30°，
    ∴∠AOB=360°-∠BOC-∠COD-∠AOD
    =360°-90°-30°-90°
    =150°．

    （2）∵EF平分∠COD，∠COD=30°，
    ∴∠DOE=∠DOC=×30°=15°，
    ∵∠AOD=90°，
    ∴∠AOF=180°-∠DOE-∠AOD=180°-15°-90°=75°，
    ∵∠AOB=150°，
    ∴直线EF平分∠AOB．
    分析：（1）代入∠AOB=360°-∠BOC-∠COD-∠AOD求出即可．
    （2）求出∠DOE，代入∠AOF=180°-∠DOE-∠AOD求出即可．
    点评：本题考查了角的有关计算和角平分线定义的应用，主要考查学生的理解能力和计算能力．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    在数学的学习中，我们要学会总结，不断地归纳，思考和运用，这样才能提高我们解决问题的能力，下面这个问题大家一定似曾相识：
    （1）比较大小：
    ①2+1
     
    2
    		2×1
    ；  ②3+
    1
    3
     
    2
    		3×
    1
    3
    ③8+8
     
    2
    		8×8

    通过上面三个计算，我们可以初步对任意的非负实数a，b做出猜想a+b
     
    2
    		ab
    ；
    （2）学习了《二次根式》后我们可以对此猜想进行代数证明，请欣赏：
    对于任意非负实数a，b，∵(
    		a
    -
    		b
    )2≥0    ，∴a-2
    		ab
    +b≥0    ，∴a+b≥2
    		ab
    ，只有当a=b时，等号成立．
    （3）学习《圆》后，我们可以对这个结论进行几何验证：
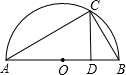
    如图，AB为半圆O的直径，C为半圆上的任意一点，（与A、B不重合）过点C作CD⊥AB，垂足为D，AD=a，DB=b．
    根据图形证明：a+b≥2
    		ab
    ，并指出等号成立时的条件．
    精英家教网
    （4）蓦然回首，我们发现在上学期的《梯形的中位线》一节遇到的一个问题，此时运用这个结论解决是那样的简单：
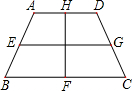
    如图有一个等腰梯形工件（厚度不计），其面积为1800cm2，现在要用细包装带如图那样包扎（四点为四边中点），则至少需要包装带的长度为
     
    cm．
    （注意：包扎时背面也有带子，打结处长度忽略不计）
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

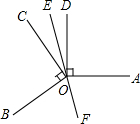    几何计算．
    如图，∠AOD=∠BOC=90°，∠COD=30°，直线EF平分∠COD．
    （1）求∠AOB的度数；
    （2）求∠AOF的度数，你发现了什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    几何计算：如图，是一副三角板重叠而成的图形，其中∠AOB和∠CDO是直角，求∠AOD+∠BOC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    几何计算：如图，是一副三角板重叠而成的图形，其中∠AOB和∠COD是直角，求∠AOD+∠BOC的度数．

    查看答案和解析>>

    同步练习册答案