
如图,在矩形ABCD中,AB=2,点E在边AD上,∠ABE=45°,BE=DE,连接BD,点P在线段DE上,过点P作PQ∥BD交BE于点Q,连接QD.设PD=x,△PQD的面积为y,则能表示y与x函数关系的图象大致是( )

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题
某校校园超市老板到批发中心选购甲、乙两种品牌的文具盒,乙品牌的进货单价是甲品牌进货单价的2倍,考虑各种因素,预计购进乙品牌文具盒的数量y(个)与甲品牌文具盒的数量x(个)之间的函数关系如图所示.当购进的甲、乙品牌的文具盒中,甲有120个时,购进甲、乙品牌文具盒共需7200元.
(1)根据图象,求y与x之间的函数关系式;
(2)求甲、乙两种品牌的文具盒进货单价;
(3)若该超市每销售1个甲种品牌的文具盒可获利4元,每销售1个乙种品牌的文具盒可获利9元,根据学生需求,超市老板决定,准备用不超过6300元购进甲、乙两种品牌的文具盒,且这两种品牌的文具盒全部售出后获利不低于1795元,问该超市有几种进货方案?哪种方案能使获利最大?最大获利为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某商店欲购进甲、乙两种商品,已知甲的进价是乙的进价的一半,进3件甲商品和1件乙商品恰好用200元.甲、乙两种商品的售价每件分别为80元、130元,该商店决定用不少于6710元且不超过6810元购进这两种商品共100件.
(1)求这两种商品的进价.
(2)该商店有几种进货方案?哪种进货方案可获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
苏科版教材中有这样一句话:“一般地,如果二次函数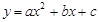 的图象与x轴有两个公共点,那么一元二次方程
的图象与x轴有两个公共点,那么一元二次方程 有两个不相等的实数根.”据此判断方程x2-2x=
有两个不相等的实数根.”据此判断方程x2-2x= -2实数根的情况是 ( )
-2实数根的情况是 ( )
| A.有三个实数根 | B.有两个实数根 | C.有一个实数根 | D.无实数根 |
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
如图,二次函数y=ax2+bx+c的图象经过(-1,0)、(0,3),下列结论中错误的是( )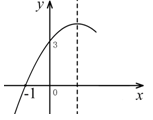
| A.abc<0 | B.9a+3b+c=0 | C.a-b="-3" | D. 4ac﹣b2<0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com