
 已知二次函数y=ax2+bx+c的图象如图所示.
已知二次函数y=ax2+bx+c的图象如图所示.分析 根据抛物线的对称轴性,抛物线的顶点坐标是(1,-1),利用待定系数法求抛物线的表达式则可.
解答 解:(1)根据题意,抛物线的顶点坐标是(1,-1),
设抛物线的表达式为y=a(x-1)2-1,
抛物线过(0,0),
所以a-1=0,a=1.
y=(x-1)2-1=x2-2x.
(2)∵y=(x-1)2-1,
∴对称轴是直线x=1;
(3)∵a=1,
∴数y有最小值,当x=1时,y的最值为-1;
(4)y=3时,x2-2x=3,
解得x=-1或3,
∴当x═-1或3时,y=3.
故答案为y=x2-2x;x=1;小,1,-1;-1或3.
点评 本题考查用待定系数法求二次函数解析式;会根据所给的函数值得到相应的自变量的值及取值.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:选择题
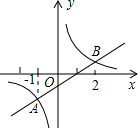 如图,一次函数与反比例函数的图象相交于A、B两点,则使得反比例函数值小于一次函数值的x的取值范围是( )
如图,一次函数与反比例函数的图象相交于A、B两点,则使得反比例函数值小于一次函数值的x的取值范围是( )| A. | x<-1 | B. | -1<x<0或x>2 | C. | x<-1或0<x<2 | D. | x>2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | AB=A′B′,BC=B′C′,∠A=∠A′ | |
| B. | ∠A=∠A′,∠B=∠B′,AC=B′C′ | |
| C. | ∠A=∠A′,∠B=∠B′,∠C=∠C′ | |
| D. | AB=A′B′,BC=B′C′,△ABC的周长等于△A′B′C′的周长 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 自来水销售价格 | 污水处理价格 | |
| 每户每月用水量 | 单价:元/吨 | 单价:元/吨 |
| 17吨及以下 | a | 0.80 |
| 超过17吨不超过30吨的部分 | b | 0.80 |
| 超过30吨的部分 | 6.00 | 0.80 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
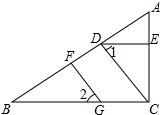 如图,若∠1=∠2,DE∥BC,则:①FG∥DC;②∠AED=∠ACB;③CD平分∠ACB;④∠1+∠B=90°;⑤∠BFG=∠BDC,其中正确的结论是( )
如图,若∠1=∠2,DE∥BC,则:①FG∥DC;②∠AED=∠ACB;③CD平分∠ACB;④∠1+∠B=90°;⑤∠BFG=∠BDC,其中正确的结论是( )| A. | ①②③ | B. | ①②⑤ | C. | ①③④ | D. | ③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com