
【题目】在一条不完整的数轴上从左到右有点A,B,C,其中AB=2,BC=1,如图所示,设点A,B,C所对应数的和是p.
(1)若以B为原点,则点A,C所对应的数分别为_____和_____,p的值为_____.若以C为原点,p的值为_____;
(2)若原点O在图中数轴上点C的右边,且CO=28,求p;
(3)若原点O在图中数轴上点C的右边,且CO=a,求p(用含a的代数式表示).
(4)若原点O在图中数轴上线段BC上,且CO=a,求p(用含a的代数式表示).利用此结果计算当a=0.5时,p的值.
![]()
【答案】(1)﹣2、1、﹣1、﹣4;(2)-88;(3)p=﹣3a﹣4;(4)p= 3a﹣4,当a=0.5时,p=﹣2.5.
【解析】
(1)根据以B为原点,则C表示1,A表示﹣2,进而得到p的值;根据以C为原点,则A表示﹣3,B表示﹣1,进而得到p的值;
(2)根据原点O在图中数轴上点C的右边,且CO=28,可得C表示﹣28,B表示﹣29,A表示﹣31,据此可得p的值.
(3)若原点O在图中数轴上点C的右边,且CO=a,可得C的值为﹣a,B的值为﹣a﹣1,A的值为﹣a﹣3,据此可得p的值;
(4)若原点O在图中数轴上线段BC上,且CO=a,可得C的值为a,B的值为﹣(1﹣a)=a﹣1,A的值为a﹣3,据此得出p的值,代入计算可得答案.
(1)若以B为原点,则点A所对应的数为﹣2、点C对应的数为1,此时p=﹣2+0+1=﹣1;
若以C为原点,则点A所对应的数为﹣3、点B对应的数为﹣1,此时p=﹣3﹣1+0=﹣4.
故答案为:﹣2、1、﹣1、﹣4;
(2)根据题意知,C的值为﹣28,B的值为﹣29,A的值为﹣31,则p=﹣28﹣29﹣31=﹣88;
(3)根据题意知,C的值为﹣a,B的值为﹣a﹣1,A的值为﹣a﹣3,则p=﹣a﹣a﹣1﹣a﹣3=﹣3a﹣4;
(4)根据题意知,C的值为a,B的值为﹣(1﹣a)=a﹣1,A的值为a﹣3,p=a+a﹣1+a﹣3=3a﹣4,当a=0.5时,p=3×0.5﹣4=﹣2.5.


科目:初中数学 来源: 题型:
【题目】每逢金秋送爽之时,正是大闸蟹上市的旺季,也是吃蟹的最好时机,可谓膏肥黄美.九月份,某经销商购进一批雌蟹、雄蟹共1000只,进价均为每只40元,然后以雌蟹每只75元、雄蟹每只60元的价格售完,共获利29000元.
(1)求该经销商分别购进雌蟹、雄蟹各多少只?
(2)民间有“九雌十雄”的说法,即九月吃雌蟹,十月吃雄蟹.十月份,在进价不变的情况下该经销商决定调整价格,将雌蟹的价格在九月份的基础上下调a%(降价后售价不低于进价),雄蟹的价格上涨 ![]() a%,同时雌蟹的销量较九月下降了
a%,同时雌蟹的销量较九月下降了 ![]() a%,雄蟹的销量上升了25%,结果十月份的销售额比九月份增加了1000元,求a的值.
a%,雄蟹的销量上升了25%,结果十月份的销售额比九月份增加了1000元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD∥BC,∠BAC=70°,DE⊥AC于点E,∠D=20°.
(1)求∠B的度数,并判断△ABC的形状;
(2)若延长线段DE恰好过点B,试说明DB是∠ABC的平分线.
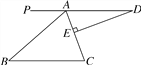
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OA交圆O于点F,则∠CBF等于( ) 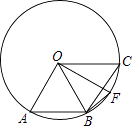
A.12.5°
B.15°
C.20°
D.22.5°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列变形中:
①由方程![]() =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;
②由方程![]() x=
x=![]() 两边同除以
两边同除以![]() ,得x=1;
,得x=1;
③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣![]() 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).
错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设三角形三个内角的度数分别为x,y,z,如果其中一个角的度数是另一个角的度数的2倍,那么我们称数对(y,z)(y≤z)是x的和谐数对.例:当x=150°时,对应的和谐数对有一个,它为(10,20);当x=66时,对应的和谐数对有二个,它们为(33,81),(38,76).当对应的和谐数对(y,z)有三个时,此时x的取值范围是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区的电力资源丰富,并且得到了较好的开发.该地区一家供电公司为了鼓励居民用电,采用分段计费的方法来计算电费.月用电量x(度)与相应电费y(元)之间的函数图像如图所示.
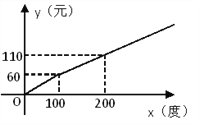
(1)月用电量为100度时,应交电费 元;
(2)当x≥100时,求y与x之间的函数关系式;
(3)月用电量为260度时,应交电费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个自然数的立方,可以分裂成若干个连续奇数的和。例如:![]() 和
和![]() 分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即
分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即![]() =3+5;
=3+5;![]() =7+9+11;
=7+9+11;![]() =13+15+17+19;…;若
=13+15+17+19;…;若![]() 也按照此规律来进行“分裂”,则
也按照此规律来进行“分裂”,则![]() “分裂”出的奇数中,最大的奇数是______.
“分裂”出的奇数中,最大的奇数是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义[p,q]为一次函数y=px+q的特征数.
(1)若特征数是[k-1,k2-1]的一次函数为正比例函数,求k的值;
(2)在平面直角坐标系中,有两点A(-m,0),B(0,-2m),且△OAB的面积为4(O为原点),若一次函数的图象过A,B两点,求该一次函数的特征数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com