
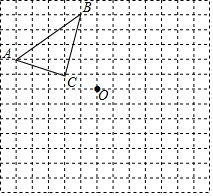
 按下列要求在方格纸中画图:
按下列要求在方格纸中画图: 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:选择题
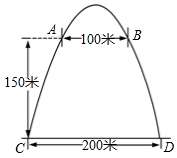 如图,拱门的地面宽度为200米,两侧距地面高150米处各有一个观光窗,两窗的水平距离为100米,则拱门的最大高度( )
如图,拱门的地面宽度为200米,两侧距地面高150米处各有一个观光窗,两窗的水平距离为100米,则拱门的最大高度( )| A. | 100米 | B. | 150米 | C. | 200米 | D. | 300米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 星期天早上,淇淇从家跑步到公园,接着马上原路步行回家,如图所示的是淇淇离家的路程y(米)与时间t(分)的函数图象,则淇淇回家的速度是每分钟步行90米.
星期天早上,淇淇从家跑步到公园,接着马上原路步行回家,如图所示的是淇淇离家的路程y(米)与时间t(分)的函数图象,则淇淇回家的速度是每分钟步行90米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
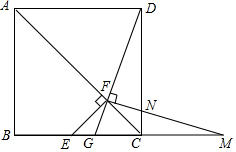 如图.在正方形ABCD中,点E是BC边上的中点,EF⊥AC于点F.连接DF并延长交BC于G.过F作FM⊥DG交CD于N,交BC的延长线于点M.
如图.在正方形ABCD中,点E是BC边上的中点,EF⊥AC于点F.连接DF并延长交BC于G.过F作FM⊥DG交CD于N,交BC的延长线于点M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
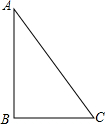 如图,Rt△ABC中,∠B=90°,AB=3,AC=5.
如图,Rt△ABC中,∠B=90°,AB=3,AC=5.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
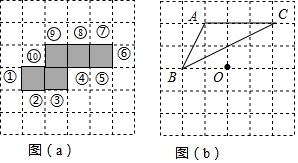
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
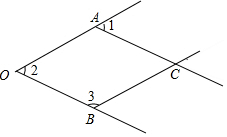 如图所示的是一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.(将下列解答过程补充完整)
如图所示的是一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.(将下列解答过程补充完整)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com