练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
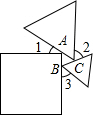
    4．如图，一个正方形和两个等边三角形的位置如图所示，若∠2=50°，则∠1+∠3=（　　）
    A．90°B．100°C．130°D．180°

    分析 根据三角形的外角和为360°列出方程即可解决问题．

    解答 解：∵正方形的内角为90°，等边三角形的内角为60°，
    又∵△ABC的外角和为360°，
    ∴（∠1+90°）+（∠2+60°）+（60°+∠3）=360°，
    ∵∠2=50°，
    ∴∠1+∠3=100°，
    故选B．

    点评 本题考查正方形的性质、等边三角形的性质、三角形的外角和定理等知识，解题的关键是利用三角形外角和等于360°列出方程解决问题，属于中考常考题型．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

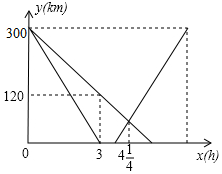    14．某客运公司的特快巴士与普通巴士同时从甲地出发，以各自的速度匀速向乙地行驶，普通巴士到达乙地后停止，特快巴士到达乙地停留45分钟后，按原路以另一速度匀速返回甲地，已知两辆巴士分别距乙地的路程y（千米）与行驶时间x（小时）之间的函数图象如图所示．求普通巴士到达乙地时，特快巴士与甲地之间的距离为187.5千米．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．如图，在Rt△ADB中，∠ADB=90°，∠A=30°，F是AB的中点，FD=3，则 BD=3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．我们知道：一元二次方程ax2+bx+c=0（a≠0）的根的情况由b2-4ac的值决定．因此，我们把b2-4ac叫一元二次方程根的判别式．看下面问题：
       例：m取何值时，方程（m+2）x2+2x-1=0有两个不相等的实数根？
    解：∵方程有两个不相等实数根
    ∴b2-4ac＞0且m+2≠0
    即：$\left\{\begin{array}{l}{4+4（m+2）＞0①}\\{m+2≠0②}\end{array}\right.$
    由①得m＞-3
    由②得m≠-2
    ∴m＞-3且m≠-2
    ∴m＞-3且m≠-2时，原方程有两个不相等实数根．
    解答下列问题：若关于x的一元二次方程kx2-（2k+1）x+k=0有实数根，求k的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．因式分解
    （1）10a（x-y）2+5ax（y-x）
    （2）（x+y）2-10（x+y）+25．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

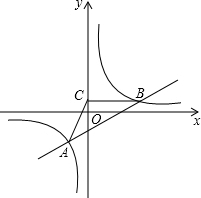    9．如图，已知双曲线y=$\frac{k}{x}$经过点B（3$\sqrt{3}$，1），点A是双曲线第三象限上的动点，过B作BC⊥y轴，垂足为C，连接AC．
    （1）求k的值；
    （2）若△ABC的面积为6$\sqrt{3}$，求直线AB的解析式；
    （3）在（2）的条件下，写出反比例函数值大于一次函数值时x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．用下列各式分别表示图中阴影部分的面积，其中表示正确的有（　　）
    ①at+（b-t）t
    ②at+bt-t2
    ③ab-（a-t）（b-t）
    ④（a-t）t+（b-t）t+t2．
    A．4个B．3个C．2个D．1个

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．已知（2x-4）2+|x+2y-8|=0，则（x-y）2017=-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．下列命题中：
    ①相等的角是对顶角；
    ②如果三角形中有一个角是钝角，那么另外两个角为锐角；
    ③若两直线平行，则内错角相等；
    ④若x＞0，则|x|=x．
    其中是真命题的有几个（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    同步练习册答案