
【题目】已知有理数a,b在数轴上的位置如图所示.
(1)在数轴上标出﹣a,﹣b的位置,并比较a,b,﹣a,﹣b的大小:
(2)化简|a+b|+|a﹣b|.
![]()
【答案】(1)图见解析,b<﹣a<a<﹣b;(2)﹣2b.
【解析】
试题(1)首先根据-a与a,-b与b互为相反数,-a与a,-b与b表示的点关于原点对称,在数轴上标出-a,-b的位置;然后根据数轴的特征:一般来说,当数轴方向朝右时,右边的数总比左边的数大,比较a,b,-a,-b的大小即可.
(2)根据有理数a,b在数轴上的位置,可得a>0>b,而且|a|<|b|,所以a+b<0,a-b>0,据此化简|a+b|+|a-b|即可.
试题解析:(1)如图所示:
![]() ,
,
b<﹣a<a<﹣b.
(2)∵a>0>b,而且|a|<|b|,
∴a+b<0,a﹣b>0,
∴|a+b|+|a﹣b|
=﹣(a+b)+(a﹣b)
=﹣a﹣b+a﹣b
=﹣2b


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC的顶点A、B在x轴上,点C在y轴上正半轴上,且
A(-1,0),B(4,0),∠ACB=90°.
(1)求过A、B、C三点的抛物线解析式;
(2)设抛物线的对称轴l与BC边交于点D,若P是对称轴l上的点,且满足以P、C、D为顶点的三角形与△AOC相似,求P点的坐标;
(3)在对称轴l和抛物线上是否分别存在点M、N,使得以A、O、M、N为顶点的四边形是平行四边形,若存在请直接写出点M、点N的坐标;若不存在,请说明理由.
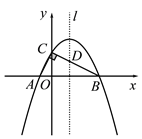
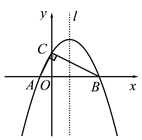
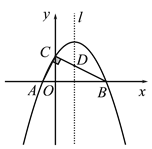
图1 备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形ABCD绕点A顺时针旋转a(0°<a<360°),得到矩形AEFG
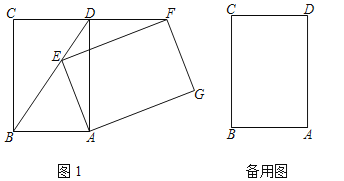
(1)如图1,当点E在BD上时求证:FD=CD;
(2)当a为何值时,GC=GB?画出图形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)
(1)画出△ABC向下平移4个单位,再向左平移1个单位得到的△A1B1C1,并直接写出C1点的坐标;
(2)作出△ABC绕点A顺时针方向旋转90°后得到的△A2B2C2,并直接写出C2点的坐标.
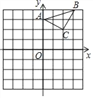
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销一种双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(单位:个)与销售单价x(单位:元)有如下关系:y=-x+60(30≤x≤60).
设这种双肩包每天的销售利润为w元.
(1)求w与x之间的函数解析式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不高于48元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,在数轴上有A,B两点,所表示的数分别为-10,4,点A以每秒5个单位长度的速度向右运动,同时点B以每秒3个单位长度的速度也向左运动,如果设运动时间为t秒,解答下列问题:![]()
(1)运动前线段AB的长为 ; 运动1秒后线段AB的长为 ;
(2)运动t秒后,点A,点B运动的距离分别为 ;用t表示A,B分别为 .
(3)求t为何值时,点A与点B恰好重合;
(4)在上述运动的过程中,是否存在某一时刻t,使得线段AB的长为6,若存在,求t的值; 若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在家中利用物理知识称量某个品牌纯牛奶的净含量,称得六盒纯牛奶的含量分别为:248mL,250mL,249mL,251mL,249mL,253mL,对于这组数据,下列说法正确的是( ).
A.平均数为251mL B.中位数为249mL
C.众数为250mL D.方差为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位长度的小正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,A,B,C三点的坐标分别为(5,﹣1),(2,﹣5),(2,﹣1).
(1)把△ABC向上平移6个单位后得到△A1B1C1,画出△A1B1C1;
(2)画出△A2B2C2,使它与△ABC关于y轴对称;
(3)画出△A3B3C3,使它与△ABC关于原点中心对称.
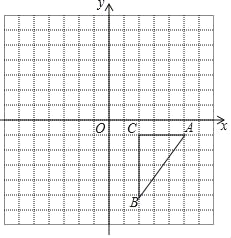
查看答案和解析>>
科目:初中数学 来源: 题型:
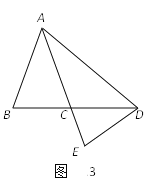
【题目】在△ABC中,∠ABC=∠ACB,点D在BC边所在的直线上,点E在射线AC上,且始终保持∠ADE=∠AED.
(1)如图1,若∠B=∠C=30°,∠BAD=70°,求∠CDE的度数;
(2)如图2,若∠ABC=∠ACB=70°,∠CDE=15°,求∠BAD的度数;
(3)如图3,当点D在BC边的延长线上时,猜想∠BAD与∠CDE的数量关系,并说明理由.
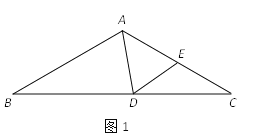
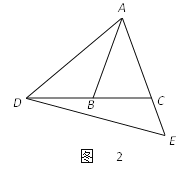
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com