
【题目】已知二次函数![]() 的部分图象如图所示,则关于
的部分图象如图所示,则关于![]() 的一元二次方程
的一元二次方程![]() 的解为 .
的解为 .

【答案】x1=-1或x2=3.
【解析】
试题分析:由二次函数y=-x2+2x+m的部分图象可以得到抛物线的对称轴和抛物线与x轴的一个交点坐标,然后可以求出另一个交点坐标,再利用抛物线与x轴交点的横坐标与相应的一元二次方程的根的关系即可得到关于x的一元二次方程-x2+2x+m=0的解.
试题解析:依题意得二次函数y=-x2+2x+m的对称轴为x=1,与x轴的一个交点为(3,0),
∴抛物线与x轴的另一个交点横坐标为1-(3-1)=-1,
∴交点坐标为(-1,0)
∴当x=-1或x=3时,函数值y=0,
即-x2+2x+m=0,
∴关于x的一元二次方程-x2+2x+m=0的解为x1=-1或x2=3.


科目:初中数学 来源: 题型:
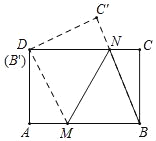
【题目】如图,四边形ABCD为矩形,将矩形ABCD沿MN折叠,折痕为MN,点B的对应点B′落在AD边上,已知AB=6,AD=4.
(1)若点B′与点D重合,连结DM,BN,求证:四边形BMB′N为菱形;
(2)在(1)问条件下求出折痕MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=![]() ,cosC=
,cosC=![]() .
.

(1)动手操作:利用尺规作以AC为直径的⊙O,并标出⊙O与AB的交点D,与BC的交点E(保留作图痕迹,不写作法);
(2)综合应用:在你所作的图中,
①求证:弧DE=弧CE ;②求点D到BC的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
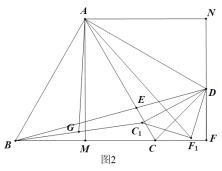
【题目】在正方形AMFN中,以AM为BC边上的高作等边三角形ABC,将AB绕点A逆时针旋转90°至点D,D点恰好落在NF上,连接BD,AC与BD交于点E,连接CD.
(1)如图1,求证:△AMC≌△AND;
(2)如图1,若DF=![]() ,求AE的长;
,求AE的长;
(3)如图2,将△CDF绕点D顺时针旋转![]() (
(![]() ),点C,F的对应点分别为
),点C,F的对应点分别为![]() 、
、![]() .连接
.连接![]() 、
、![]() ,点G是
,点G是![]() 的中点,连接AG.试探索
的中点,连接AG.试探索![]() 是否为定值,若是定值,则求出该值;若不是,请说明理由.
是否为定值,若是定值,则求出该值;若不是,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖和同学一起去书店买书,他们先用60元买了一种科普书,又用60元买了一种文学书.科普书的价格比文学书高出一半,他们所买的科普书比所买的文学书少2本.
(1)求他们买的科普书和文学书的价格各是多少元?
(2)学校某月开展读书活动,班上同学让小颖帮助购买科普书和文学书共20本,且购买总费用不超过260元,求小颖至少购买多少本文学书?
查看答案和解析>>
科目:初中数学 来源: 题型:
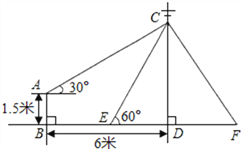
【题目】如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角
∠CED=60°,在离电线杆6米的B处安置测角仪AB,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长 (结果精确到0.1米,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732).
≈1.732).
查看答案和解析>>
科目:初中数学 来源: 题型:
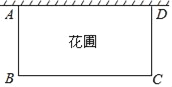
【题目】为了美化生活环境,小兰的爸爸要在院墙外的一块空地上修建一个矩形花圃.如图所示,矩形花圃的一边利用长10米的院墙,另外三条边用篱笆围成,篱笆的总长为32米.设AB的长为x米,矩形花圃的面积为y平方米.
(1)用含有x的代数式表示BC的长,BC= ;
(2)求y与x的函数关系式,写出自变量x的取值范围;
(3)当x为何值时,y有最大值?最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用三角形和六边形按如图所示的规律拼图案.

(1)第4个图案中,三角形有______个,六边形有______个;
(2)第![]() (
(![]() 为正整数)个图案中,三角形与六边形各有多少个?
为正整数)个图案中,三角形与六边形各有多少个?
(3)第2019个图案中,三角形与六边形共有多少个?
(4)是否存在某个符合上述规律的图案,其中有100个三角形与48个六边形?如果有,指出是第几个图案;如果没有,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳生活,绿色出行”,2017年1月,某公司向深圳市场新投放共享单车640辆.
(1)若1月份到4月份新投放单车数量的月平均增长率相同,3月份新投放共享单车1000辆.请问该公司4月份在深圳市新投放共享单车多少辆?
(2)考虑到自行车市场需求不断增加,某商城准备用不超过70000元的资金再购进A,B两种规格的自行车100辆,已知A型的进价为500元/辆,售价为700元/辆,B型车进价为1000元/辆,售价为1300元/辆。假设所进车辆全部售完,为了使利润最大,该商城应如何进货?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com