
| A. | $\frac{1}{2^{98}}$尺 | B. | $\frac{1}{2^{99}}$尺 | C. | $\frac{1}{2^{100}}$尺 | D. | $\frac{1}{{2}^{101}}$尺 |
分析 根据题意,利用乘方的意义确定出剩下的长度即可.
解答 解:第1次截取其长度的一半,剩下长度为$\frac{1}{{2}^{1}}$×1=$\frac{1}{2}$尺,
第2次截取其第1次剩下长度的一半,剩下的长度为$\frac{1}{{2}^{2}}$×1=$\frac{1}{4}$尺,
第3次截取其第2次剩下长度的一半,剩下的长度为$\frac{1}{{2}^{3}}$×1=$\frac{1}{8}$尺,
如此反复,
第99次截取后,木杆剩下的长度为$\frac{1}{{2}^{99}}$×1=$\frac{1}{{2}^{99}}$(尺),
则此木杆剩下的长度为$\frac{1}{{2}^{99}}$尺.
故选B
点评 此题考查了有理数的乘方,熟练掌握乘方的意义是解本题的关键.


 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
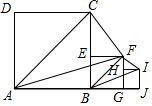 如图,已知四边形ABCD,BEFG,GHIJ都是正方形,E为BC边上的动点,H为FG的中点,若AB=1,记BE=x,△ACF与△BFI的面积之和为y,则y关于x的函数图象正确的是( )
如图,已知四边形ABCD,BEFG,GHIJ都是正方形,E为BC边上的动点,H为FG的中点,若AB=1,记BE=x,△ACF与△BFI的面积之和为y,则y关于x的函数图象正确的是( )| A. | 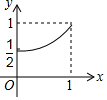 | B. | 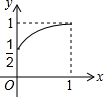 | C. | 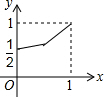 | D. | 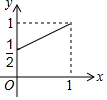 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
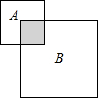 如图所示,在桌面上放着A、B两个正方形,共遮住的面积为21cm2.若这两个正方形折叠部分(阴影部分)的面积为3cm2,且正方形B除重叠部分外的面积是正方形A除重叠部分外的面积的2倍,则正方形A的面积是9cm2.
如图所示,在桌面上放着A、B两个正方形,共遮住的面积为21cm2.若这两个正方形折叠部分(阴影部分)的面积为3cm2,且正方形B除重叠部分外的面积是正方形A除重叠部分外的面积的2倍,则正方形A的面积是9cm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com