
【题目】如图,在矩形![]() 中,点
中,点![]() 是
是![]() 的中点,
的中点,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,将
,将![]() 沿
沿![]() 折叠,点
折叠,点![]() 恰好落在
恰好落在![]() 上
上![]() 点处,延长
点处,延长![]() ,
,![]() 交于点
交于点![]() .有下列四个结论:①
.有下列四个结论:①![]() 垂直平分
垂直平分![]() ;②
;②![]() 平分
平分![]() ;③
;③![]() ;④
;④![]() .其中,将正确结论的序号全部选对的是( )
.其中,将正确结论的序号全部选对的是( )
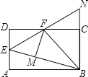
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
【答案】A
【解析】
由折叠的性质、矩形的性质与角平分线的性质,可证得CF=FM=DF;易求得∠BFE=∠BFN,则可得BF⊥EN;易证得△BEN是等腰三角形,但无法判定是等边三角形;故正确的结论有3个.
解:∵四边形ABCD是矩形,
∴∠D=∠BCD=90°,DF=MF,
由折叠的性质可得:∠EMF=∠D=90°,
即FM⊥BE,CF⊥BC,
∵BF平分∠EBC,
∴CF=MF,
∴DF=CF,在△DEF与△CFN中,
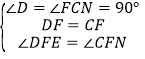
∴△DFE≌△CFN,
∴EF=FN,
∵∠BFM=90°∠EBF,∠BFC=90°∠CBF,
∴∠BFM=∠BFC,
∴BF平分∠MFC;故②正确;
∵∠MFE=∠DFE=∠CFN,
∴∠BFE=∠BFN,
∵∠BFE+∠BFN=180°,
∴∠BFE=90°,
即BF⊥EN,
∴BF垂直平分EN,故①正确;
∵∠BFE=∠D=∠FME=90°,
∴∠EFM+∠FEM=∠FEM+∠FBE=90°,
∴∠EFM=∠EBF,
∵∠DFE=∠EFM,
∴∠DFE=∠FBE,
∴△DEF∽△FEB;故③正确;
∵△DFE≌△CFN,∴BE=BN,
∴△EBN是等腰三角形,
∴∠N不一定等于60°,
故④错误.
故答案选:A.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
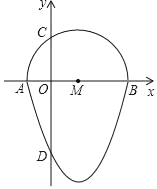
【题目】如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点,抛物线的解析式为y=x2﹣6x﹣16,AB为半圆的直径,则这个“果圆”被y轴截得的线段CD的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为庆祝建党90周年举行唱“红歌”比赛,已知10位评委给某班的打分是:8,9,6,8,9,10,6,8,9,7.
(1)求这组数据的极差:
(2)求这组数据的众数;
(3)比赛规定:去掉一个最髙分和一个最低分,剩下分数的平均数作为该班的最后得分.求该班的最后得分.
查看答案和解析>>
科目:初中数学 来源: 题型:
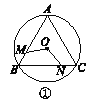
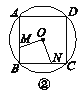
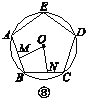
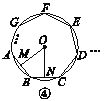
【题目】如图①②③④,M,N分别是⊙O的内接正三角形ABC,正方形ABCD,正五边形ABCDE,…,正n边形ABCDEFG…的边AB,BC上的点,且BM=CN,连接OM,ON.
(1)求图①中∠MON的度数;
(2)图②中,∠MON的度数是________,图③中∠MON的度数是________;
(3)试探究∠MON的度数与正n边形的边数n的关系(直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆内接四边形ABCD的BA,CD的延长线交于P,AC,BD交于E,则图中相似三角形有( )
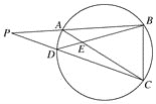
A. 2对 B. 3对 C. 4对 D. 5对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC和△DEF中,若∠A=∠D,则下列四个条件:①![]() =
=![]() ;②
;②![]() =
=![]() ;③∠B=∠F;④∠E=∠F中,一定能推得△ABC与△DEF相似的共有( )
;③∠B=∠F;④∠E=∠F中,一定能推得△ABC与△DEF相似的共有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
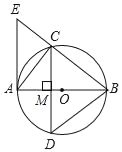
【题目】如图,△BCD内接于⊙O,直径AB经过弦CD的中点M,AE交BC的延长线于点E,连接AC,∠EAC=∠ABD=30°.
(1)求证:△BCD是等边三角形;
(2)求证:AE是⊙O的切线;
(3)若CE=2,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com